gnomonic

gnomic

horologium

central

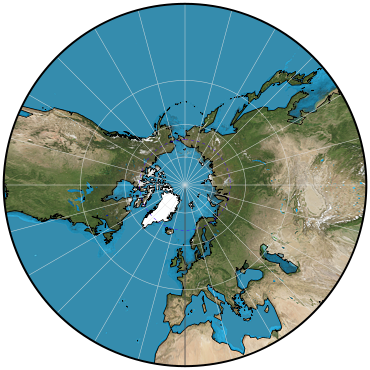
Classifications

azimuthal
perspective

Graticule

Polar aspect:.
Meridians: Equally spaced straight lines intersecting at the central pole. Angles between them are the true angles.
Parallels: Unequally spaced circles centered at the pole, which is a point. The equator and the opposite hemisphere cannot be shown. Spacing increases rapidly away from the pole.
Symmetry: About any meridian.
Equatorial aspect:.
Meridians: Unequally spaced straight parallel lines. Only meridians within 90° of the central meridian can be shown. Spacing increases away from the central meridian.
Parallels: Equator is a straight line perpendicular to the meridians. Other parallels are hyperbolic arcs concave toward the nearest pole. Spacing increases rapidly away from the equator. Poles cannot be shown.
Symmetry: About the central meridian or the equator.
Oblique aspect:.
Meridians: Unequally spaced straight lines intersecting at the pole nearest the center of the projection.
Parallels: Equator is a straight line perpendicular to the central meridian. If the central parallel is a north latitude, its colatitude (90°-central latitude) is shown as a parabolic arc, more northern parallels are ellipses, and more southern parallels are hyperbolas, all concave toward the nearest pole. If the central parallel is a south latitude, opposite signs apply.
Symmetry: About the central meridian.

Range

Less than one hemisphere centered on a given pole of projection or map origin.

Scale

True only where the central parallel crosses the central meridian. Increases rapidly with the distance from the center.

Distortion

Only the center is free from distortion. Distortion increases rapidly away from the center.

Special features

All great circles (including all meridians and the equator) are shown as straight lines. Therefore, the path of the shortest distance between any two points on the map is a straight line.
Perspective projection from the center of the globe onto a plane tangent at the central point of projection.
Less than a hemisphere can be shown on one map.

Usage

To show great-circle paths as straight lines and thus to assist navigators and aviators in determining appropriate courses. Too much distortion of many kinds for regular geographic maps. Used in the past for some star maps and for world globes in the shapes of polyhedra.

Similar projections

Two-Point azimuthal projection is a Gnomonic projection that has been compressed in one direction.

Origin

Possibly developed by Thales (c. 580 B.C.) of Greece. Name derived from the gnomon of a sundial, since meridians radiate like the hour markings on a sundial.

Description adapted from J.P. Snyder and P.M. Voxland, An Album of Map Projections, U.S. Geological Survey Professional Paper 1453. United States Government Printing Office: 1989.