Requisite physiographic map. That big white plus sign? Just ignore that.
— daan
On distortion and optimal projections
Re: On distortion and optimal projections
I know I felt that the Dietrich-Kitada projection was far from optimal, but this projection indeed even looks like it could be optimal.
Given the popularity of equal-area projections, and of uninterrupted projections (as commonly termed, yes, the "edge" of a map certainly is an interruption of sorts), if there is an analytic description of this projection (apparently at the moment the coordinates have simply resulted from the optimization process, if I understand your post correctly), it could be very popular. You may even be applying, or advised to apply, for a patent on this projection in this case.
I could see it on classroom walls and in atlases very soon, I think. Congratulations on a noteworthy achievement!
Given the popularity of equal-area projections, and of uninterrupted projections (as commonly termed, yes, the "edge" of a map certainly is an interruption of sorts), if there is an analytic description of this projection (apparently at the moment the coordinates have simply resulted from the optimization process, if I understand your post correctly), it could be very popular. You may even be applying, or advised to apply, for a patent on this projection in this case.
I could see it on classroom walls and in atlases very soon, I think. Congratulations on a noteworthy achievement!
Re: On distortion and optimal projections
Incidentally, I noticed that your projection, while it didn't resemble the Dietrich-Kitada projection much to me, did have quite a resemblance to Tobias Jung's modification of the Hammer projection.
If, instead of reducing the stretch factor from 2 to 1.2, as he did, one reduces it less, to 1.3333... or 1 1/3, one obtains the following:
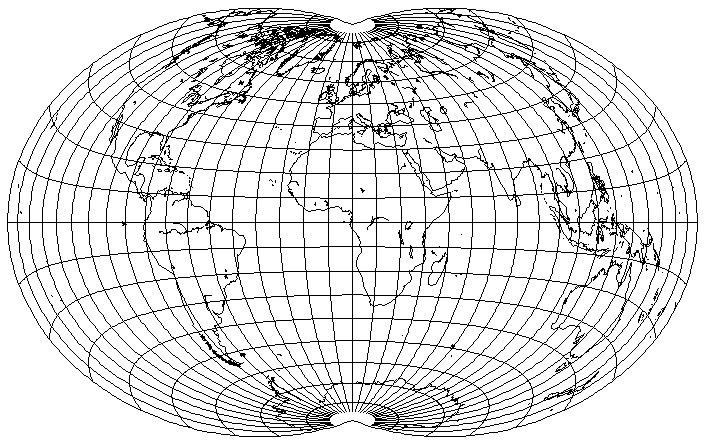
which has at least a superficial resemblance to the optimal equal-area projection which you have devised.
It looked nice enough that I wondered what would be the result if I used the orientation for Bartholomew's Nordic projection:
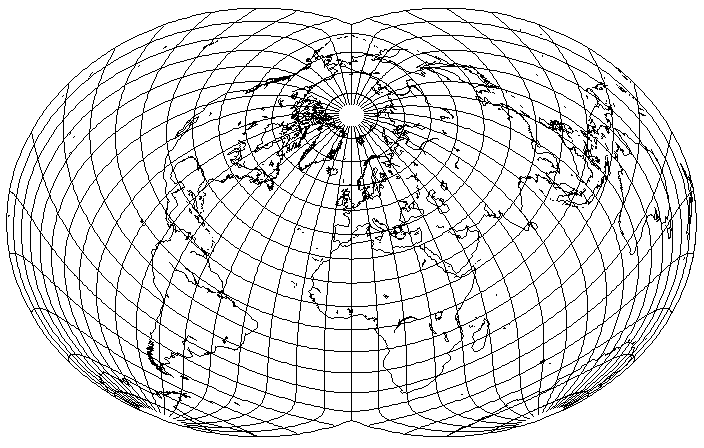
Everything looks nice... except Australia and New Zealand. Of course, one could change the central meridian to try to improve things:
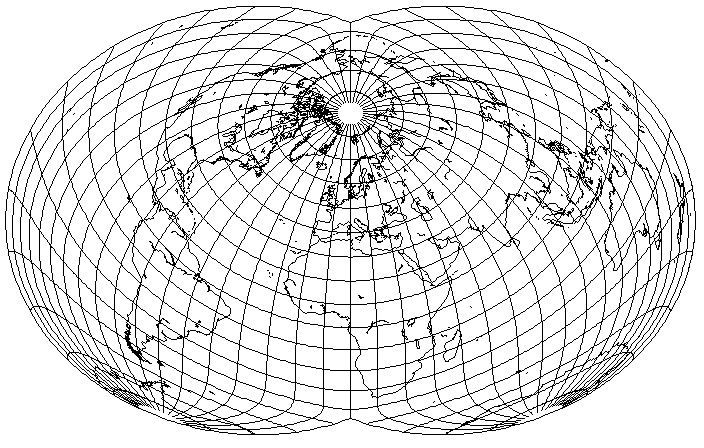
helps a bit, although at least people living in Australia might think this is more balanced:
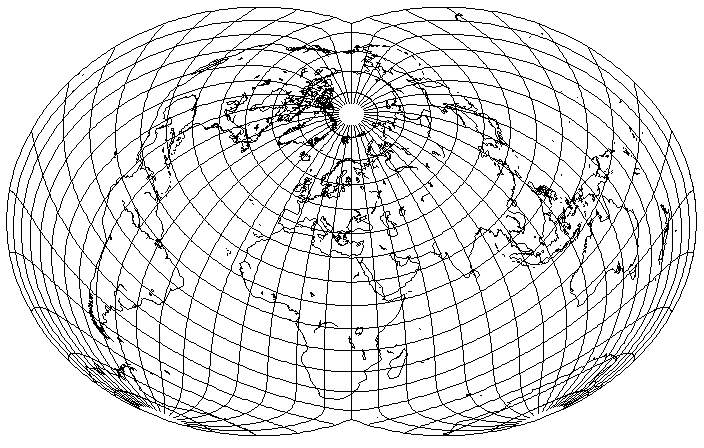
If, instead of reducing the stretch factor from 2 to 1.2, as he did, one reduces it less, to 1.3333... or 1 1/3, one obtains the following:

which has at least a superficial resemblance to the optimal equal-area projection which you have devised.
It looked nice enough that I wondered what would be the result if I used the orientation for Bartholomew's Nordic projection:

Everything looks nice... except Australia and New Zealand. Of course, one could change the central meridian to try to improve things:

helps a bit, although at least people living in Australia might think this is more balanced:

Last edited by quadibloc on Mon Apr 20, 2020 9:53 pm, edited 1 time in total.
Re: On distortion and optimal projections
Although there is a superficial resemblance between your optimal projection and a variant of the Hammer such as what I showed, I see now, after making a closer comparison, that your optimal projection is significantly different.
For one thing, as I increase the aspect ratio, making the projection wider in proportion to its height, the degree to which the poles are indented decreases. Your projection is both wider and more indented than mine, so it's not on the same continuum there.
Even more importantly, while the stretch at the meridian where it is interrupted somewhat resembles that on a Hammer-based projection, it is significantly less, at least for all but the extreme Arctic and Antarctic latitudes.
For one thing, as I increase the aspect ratio, making the projection wider in proportion to its height, the degree to which the poles are indented decreases. Your projection is both wider and more indented than mine, so it's not on the same continuum there.
Even more importantly, while the stretch at the meridian where it is interrupted somewhat resembles that on a Hammer-based projection, it is significantly less, at least for all but the extreme Arctic and Antarctic latitudes.
Re: On distortion and optimal projections
Thanks for the kind words, John. When I get the differential conditions more cleanly expressed, I hope some closed-form formulation will fall out of it. That would be a fabulous outcome.
I think patenting a map projection is the best way to ensure that it does not get used!

The Hammer parameterizations were some of the “smoke tests” I used to confirm that my generated projection had lower maximum angular deformation than anything else. The original one you posted looks alarmingly close, but as you noticed, the outer meridians at the central latitudes carry a fair bit more distortion. As an artifact of the constant scale along the outer boundary and the constant spacing of latitudes on earth, the projected parallels get spaced constantly at the outer meridian. That part gets most obviously corrupted by Hammer.
The big, white plus sign and rest of the mess toward the middle turned out to be a simple coding error. Here’s something a little more refined, and with your proposed aspect. No real improvement over land with the tilted optimal one because this centering moves all the land away from the higher distortion areas. Hammer fares a little better for southern Africa; optimal projection fares a little better for east Asia; South America, Australia, New Zealand are draws. North America depends on region, but optimal projection has somewhat less over all.
I still have a fair amount of cleaning up to do before it’s ready for prime time. Also, 2D interpolation really is annoying for non-conformal maps, I have to say. What I’m doing here is not suited to kriging or radial basis functions on the one end, nor to bilinear/bicubic-style polynomial interpretation, on the other end. It’s in between those extremes, and I’m just not finding anything good in that space.
Cheers.
— daan
I think patenting a map projection is the best way to ensure that it does not get used!
The Hammer parameterizations were some of the “smoke tests” I used to confirm that my generated projection had lower maximum angular deformation than anything else. The original one you posted looks alarmingly close, but as you noticed, the outer meridians at the central latitudes carry a fair bit more distortion. As an artifact of the constant scale along the outer boundary and the constant spacing of latitudes on earth, the projected parallels get spaced constantly at the outer meridian. That part gets most obviously corrupted by Hammer.
The big, white plus sign and rest of the mess toward the middle turned out to be a simple coding error. Here’s something a little more refined, and with your proposed aspect. No real improvement over land with the tilted optimal one because this centering moves all the land away from the higher distortion areas. Hammer fares a little better for southern Africa; optimal projection fares a little better for east Asia; South America, Australia, New Zealand are draws. North America depends on region, but optimal projection has somewhat less over all.
I still have a fair amount of cleaning up to do before it’s ready for prime time. Also, 2D interpolation really is annoying for non-conformal maps, I have to say. What I’m doing here is not suited to kriging or radial basis functions on the one end, nor to bilinear/bicubic-style polynomial interpretation, on the other end. It’s in between those extremes, and I’m just not finding anything good in that space.
Cheers.
— daan
Re: On distortion and optimal projections
Of course, since your projection has less stretch at the edges on the Equator of the projection, the large rotation I needed to help Australia isn't relevant to your projection. You should probably have gone with the 10 degree rotation instead of the 30 degree rotation, like this when I use a longitude compression of 1.5 for the Lambert Azimuthal Equal-Area:


Re: On distortion and optimal projections
The distortion characteristics of the two projections are quite similar all over Australia in the 10°E centering. The optimal projection has a slight advantage, but it’s not enough to notice. It would only be by crowding Australia up against the edge of the map that the optimal projection’s merits are visible—not that it’s any better than a mess even so!
Cheers.
— daan
Cheers.
— daan
-
Atarimaster
- Posts: 449
- Joined: Fri Nov 07, 2014 2:43 am
Re: On distortion and optimal projections
Coming back from a brief holiday, I see I missed some interesting stuff…
Nice work on the Optimal equal-area!
Nice work on the Optimal equal-area!
-
dummy_index
- Posts: 28
- Joined: Sat Dec 21, 2019 12:38 pm
Re: On distortion and optimal projections
How about Hammer without stretching?
 longitude halving -> Lambert azimuthal equal-area -> scale 1.4x in x and y (to restore area)
longitude halving -> Lambert azimuthal equal-area -> scale 1.4x in x and y (to restore area)
Maximum angular deformation is about 74°. (unconfident)
Needless to say, Eisenlohr projection is a projection least area-error in the meaning of "infinity norm." In contrast, attempt to minimize "Entire strain energy" is "Euclidean norm" context and may lead differ answer (parhaps August projection, or maybe Lagrange projection.)
Maximum angular deformation is about 74°. (unconfident)
Needless to say, Eisenlohr projection is a projection least area-error in the meaning of "infinity norm." In contrast, attempt to minimize "Entire strain energy" is "Euclidean norm" context and may lead differ answer (parhaps August projection, or maybe Lagrange projection.)
Last edited by dummy_index on Wed Jan 08, 2020 9:03 am, edited 1 time in total.
Re: On distortion and optimal projections
One thing that I perhaps should have said explicitly: although my attempts to imitate your projection with trivial variations on the Hammer projection weren't successful, it appears to me that your projection has such a strong resemblance to the Hammer that one could probably come up with an empirical modification of the Hammer that comes very close to it, even if it isn't an exact match. That would allow for a projection with a closed form description that at least closely approaches optimality.