Some speculations about Dietrich-Kitada

[quadibloc]

Oh, and by the way, I tried to "fix" the Dietrich-Kitada by giving it a 25% horizontal stretch, to obtain this:



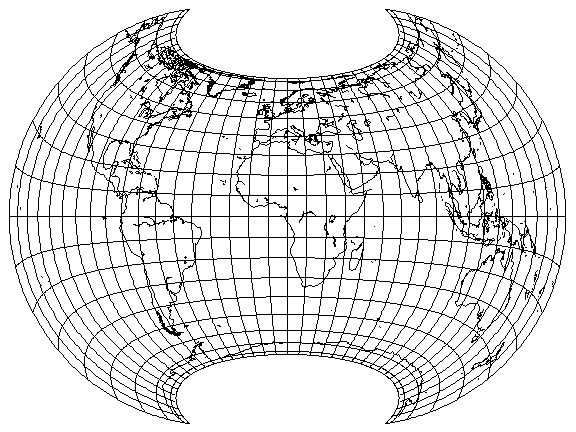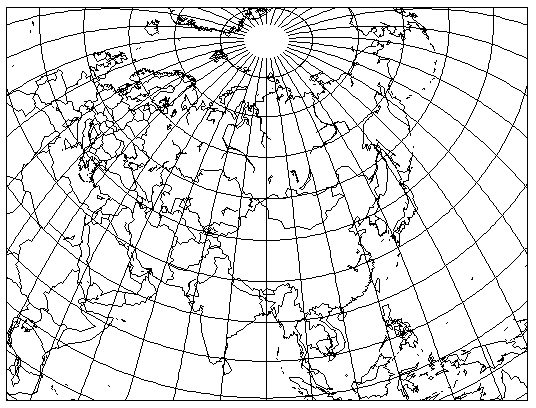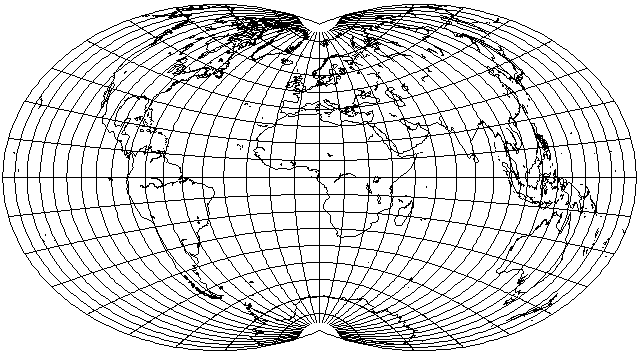
While in a way it sort of "looks better", my overall assessment was that if I seriously proposed this for use as a world map, people would laugh at me. But perhaps I'm not being objective.

[daan]

but I like the overall distribution of distortion better on Dietrich–Kitada.

You do? I find the Dietrich-Kitada interesting, and so I toyed with extracting a useful projection from its central hemisphere, but in general I've found "the general distribution of distortion" of the Dietrich-Kitada to be its greatest flaw, making it almost impossible to find an orientation of the world on that projection that makes an attractive map, with the high distortion all dumped in the middle of the ocean.

I was speaking in an academic way, not in a mapmaker way.


— daan

[quadibloc]

I was speaking in an academic way, not in a mapmaker way.

Oh. In that case, I agree with you. As noted, while I wasn't happy with the direct usefulness of the projection, its... distinctiveness... suggests that there's a way to tease out of it a projection that would be very useful in the mapmaker sense.

[quadibloc]

The outer shape is somewhat similar, and it is fully equal-area, but the graticule (and there, the distribution of distortion) is totally different. So in fact… it’s not very much like Dietrich-Kitada.

When I endeavored to duplicate your projection, I found that you had to reduce the stretch from 2, as in the Hammer projection, all the way down to 1.2 in order to get an apple shape.

This gave me some inspiration: while the shape obtained by reducing the stretch only to 1.5 was a sort of slightly apple-shaped outline which people would find strange, perhaps it might work well with short pole-lines:



I even tried an asymmetric version:

[Atarimaster]

When I endeavored to duplicate your projection, I found that you had to reduce the stretch from 2, as in the Hammer projection, all the way down to 1.2 in order to get an apple shape.

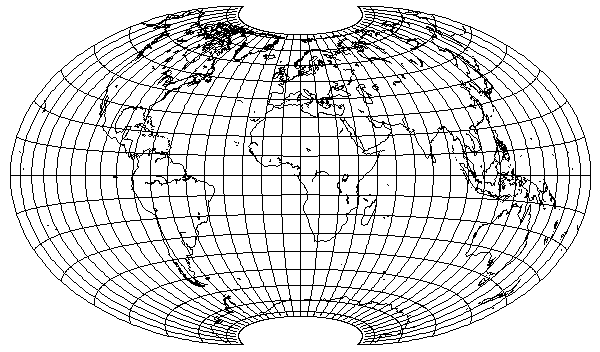
Yes, my goal here was that the point at the center of the map should have no angular deformation. I came close but did not achieve this totally. However to find the exact parameters would have been a lot of “try & err” for me, and since Geocart offers an “undistorted location” feature, I stopped there.

This gave me some inspiration: while the shape obtained by reducing the stretch only to 1.5 was a sort of slightly apple-shaped outline which people would find strange, perhaps it might work well with short pole-lines:

Nice, but…
Dr. Rolf Böhm came up with a very similar variation [1][2] (his pole lines are a bit longer and the curcature of the parallels is a bit less pronounced):

wagner-boehm-2.png (156.26 KiB) Viewed 1854 times

I even tried an asymmetric version

Nice again!


[1] Dr. Böhm showing his variant on his German website: http://www.boehmwanderkarten.de/kartogr ... rld_3.html
[2] Dr. Böhm’s first presentation of this variant, from the German journal “Karthographische Nachrichten”: http://www.boehmwanderkarten.de/archiv/ ... mplete.pdf

[quadibloc]

Dr. Rolf Böhm came up with a very similar variation [1][2] (his pole lines are a bit longer and the curcature of the parallels is a bit less pronounced)

The one variation you show doesn't seem to be based on something apple-shaped; instead, it seems to be based on the ellipse.

But it is very interesting none the less. I see from his paper that the variation he calls 60-132-60-0-200, as well as 57-105-60-20-200 with longer pole lines, have nearly rectangular regions of lower distortion in the center. That, of course, is of great interest for continental maps.

[Atarimaster]

The one variation you show doesn't seem to be based on something apple-shaped; instead, it seems to be based on the ellipse.

I didn’t want to claim that it was based on something apple-shaped (in case it seemed that way), but I found it interesting that you two arrive at almost the same point, coming from two different sides – in a manner of speaking.

But it is very interesting none the less. I see from his paper that the variation he calls 60-132-60-0-200, as well as 57-105-60-20-200 with longer pole lines, have nearly rectangular regions of lower distortion in the center. That, of course, is of great interest for continental maps.

Yes, you got exactly his point, without even knowing the language!

[quadibloc]

I didn’t want to claim that it was based on something apple-shaped (in case it seemed that way), but I found it interesting that you two arrive at almost the same point, coming from two different sides – in a manner of speaking.

It turns out I was wrong, and it is based on something apple-shaped. The second parameter in his notation, "132", as opposed to 90 for the Hammer and 60 for the Wagner VII, means (I think; I used Google Translate on his page to understand his notation) that he is using what I refer to as a longitude compression factor of 1.46666... which is very similar to the 1.5 that I had used.

60-132-60-0-200 means, as best as I can decipher:

The latitude compression factor, from imposing one cylindrical equal-area projection on another (in the equal-area case) is the sine of 60 degrees;

132 degrees of longitude of the Lambert Azimuthal Equal-Area are used as the field of the projection (this is 11/15 of 180 degrees, 180 degrees is the Lambert, 90 degrees the Hammer, 60 degrees the Wagner VII, 45 degrees the Eckert-Grieffendorff). I guess this is 0 for pseudocylindricals.

60-0 as the third and fourth parameters mean that the projection is equal area. I would not even try to guess how one determines a projection that is not equal area from those parameters. (It reports that there is 0% areal exaggeration at 60 degrees latitude compared to the Equator. The only case I understand is where the exaggeration reported matches equidistant parallels.)

200 is the ratio, as a percentage, between the actual widths of the Equator and the central meridian as seen on the final projection, so it is complicated to calculate. In the case of 60 and 132 as the first two parameters, this leads to a vertical stretch of about 7% in the center of the projection, having determined it graphically rather than carrying out the equations for Lambert's Azimuthal Equal-Area to determine it exactly.

Actually, I see from your error curves that this one is not the one I had found interesting. In any case, I found his
60-132-60-0-200 interesting enough to mention it on my web site, together with my recreation of both the world map



and the map of Eurasia:

[Atarimaster]

You got the meanings of the numbers (60-132-60-0-200 etc.) right, but it works different from what I think that you think…
The numbers basically represent the values that Wagner used to conduct the Umbeziffern, I wrote a little article about this and Dr. Böhm’s notation:
https://map-projections.net/wagner-umbeziffern.php

In Böhm’s paper, the formulae 7 - 12 show how to convert the values to values that are used to render the projection.