What is shear in map projections?

[RogerOwens]

For me, the defining characteristic of a conformal projection is that, at any particular point on the map, the scale is the same in every direction.

So, when deforming a slit globe into a conformal flat map, the expansion or compression at any point must be by the same factor in every direction. By suitable choice of which points to expand or compress by which amounts, the globe can be deformed into a conformal flat map.

No sliding needed.

Michael Ossipoff
August 21st
35 W
0328 UTC

[quadibloc]

You can’t say that about any other projection, if I understand what you’re saying. The phenomenon is specific to sinusoidal, due to its correct scale along parallels.

Yes. A Mollweide mixes shear with stretching, an Eckert IV has less shear and more stretching, and a Behrmann is all stretching. Shear may be a subjective concept - but, hey, what uses maps? People!

The Bonne projection does do the same thing - because it's another form of the Sinusoidal projection. But the way it's usually used, a Bonne map of a continent won't hit you in the face with its nature the way an interrupted Sinusoidal map of the world would. But if the self-correcting property were recognized as important, one could imagine an atlas which both used the Bonne projection, and had a little explanation in the front of how to make the best use of it - what to look for in the graticule that tells you what's going on.

As I pointed out, the Orthographic is also "self-correcting" - but by means of another completely different mechanism.

And I have now come up with a third fundamental example of a self-correcting projection. The Transverse Mercator. Not the regular Mercator, only the Transverse Mercator.

Huh?

Well, look at a map drawn on the Transverse Mercator:



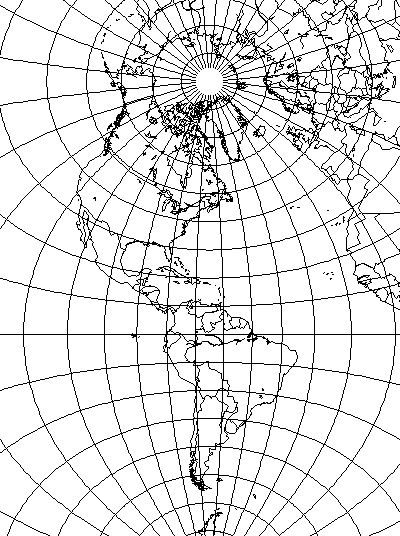
Because the central meridian includes every degree of latitude, one can reference the latitude and longitude quadrangles in which enlarged portions of the map are located to similar quadrangles at the same latitude on the central meridian, and immediately see how much they have to be shrunk down to make them right. Since a meridian is a great circle, and a parallel other than the Equator is a small circle, I can't make this work for a conformal conic.

Come to think of it, one could well argue that the polyconic, or Cassini's projection, or any other projection with a central meridian that is conformal and at constant scale, is self-correcting in this way as well; the shape of the quadrangles of latitude and longitude is an immediate guide to the amount by which any other quadrangle at the same latitude has to be altered... in both shape and size, in the case of such a projection which is neither conformal nor equal-area. The Sinusoidal, and then the Transverse Mercator, are merely the two easiest cases of this, because with only one distortion to account for, it's simpler to see the change that needs to be made.

[RogerOwens]

A Mollweide mixes shear with stretching, an Eckert IV has less shear and more stretching, and a Behrmann is all stretching.

.
Yes, it’s a common misconception that “shear” refers to nonperpendicularity of grid-lines, and that the disproportion due to different NS & EW scales isn’t shear.
.
But it’s been explained to you here by two people that, by its meaning universally used by cartographers and people who communicate with them, shear doesn’t refer to nonperpendicularity of grid-lines, and any non-conformal map has shear, and every cylindrical projection other than Mercator has shear, and every pseudocylindrical projection has shear, and, if, at some point, the NS scale is different from the EW scale, then there’s shear.
.
As I said before, sometimes nonperpendicularity of grid-lines, of itself, is of interest. And sometimes it’s of interest just because it’s one of the indicators of shear. But, when referring specifically to graticule-intersection nonperpendicularity, I don’t call it “shear”. I call it “slant”. …to distinguish it from shear.
.
As I said, where there’s slant, there’s shear, but there can be shear without slant (as there is in all cylindricals other than Mercator.
.
Actually, the cartographers’ definition of shear is completely consistent with, and the same as, the engineer’s definition of shear.
.
If, within a 3D solid material, there’s a plane across which there’s relative motion or displacement parallel to the plane, that’s shear. Likewise, if on a 2D surface, there’s a line across which there’s relative motion or displacement parallel to the line, that’s shear.
.
That’s what shear means. That’s what shear means in cartography, and that’s what shear means in engineering.
.
And, as I said, by that definition, every cylindrical other than Mercator has shear.
.
And every nonconformal map has shear.
.
And anytime, at some point, the NS scale differs from the EW scale, there’s shear.
.
Michael Ossipoff
37 Sa
September 7th
0336 UTC

[quadibloc]

As I said before, sometimes nonperpendicularity of grid-lines, of itself, is of interest. And sometimes it’s of interest just because it’s one of the indicators of shear. But, when referring specifically to graticule-intersection nonperpendicularity, I don’t call it “shear”. I call it “slant”. …to distinguish it from shear.

Then, indeed, "slant" is what I am talking about. Since there are already terms for what you call "shear", angular error, distortion, or deformation, it's not as if I am without a word to use to refer to general angular error, whereas using the word shear for that, due to the common misconception, is confusing.

But it’s been explained to you here by two people

The other thing is that I took Daniel Strebe's posting as an expression of a personal view, growing out of a situation where the term "shear" does not have a meaningful or consistent definition within cartography. And I agreed with what I took to be his view: that "shear" in the popular sense was not a well-defined concept that is normally very useful in cartography, while angular error is a consistent and well-defined concept. I also accepted his statement that there were at least some contexts in which shear could be taken as a term for angular distortion in general.

So, perhaps mistakenly on my part, I had not perceived him as holding the same view that you are expressing here: that any use of the term "shear" for anything else but angular error in general is simply wrong, and, thus, is absolutely to be avoided.

[RogerOwens]

Quadibloc--

First I want to emphasize that, before daan posted this thread, I too thought that shear was the same as slant. So have other posters here. So I made the same mistake, and so I’m not suggesting that your mistake is criticizable by me.
.
You wrote:
.

Since there are already terms for what you call "shear", angular error, distortion, or deformation, it's not as if I am without a word to use to refer to general angular error, whereas using the word shear for that, due to the common misconception, is confusing.

.
True. Daan pointed out that shear, angular error, shape-disproportion, deformation, are all different descriptions of the same thing, just numerically-different descriptions of the same thing.
.
So yes, maybe the word “shear” is best avoided in general discussion, because there are those other better-known terms.
.
Which do I prefer? Shape-disproportion and scale-variation. They’re the same thing, of course.
.
One nice thing about scale-variation is that it’s useful for comparison across all kinds of projections, since it’s the standard for comparing conformal projections as well.
.
I also like min-scale, out to North-Cape, or the average, over the whole map, of the smallest scale at each of the map’s points. …with either of those referenced to, divided by, the map’s largest X dimension or Y dimension, depending on which of those is critical to the map’s fit to the available display-space. (or their geometric-mean if it the fit-situation isn’t known in advance). But I seem to be the only person who likes that those standards.
.
Also, a projection’s “space-efficiency” (the % of its circumscribing-rectangle that it fills) is of interest to me. …or sometimes the square-root of map-area divided by the largest X or Y dimension, depending on the fit-situation.
.
It’s been pointed out that all those different standards, together, are a lot less useful for consistent comparison, as opposed to just using overall min-scale/max-scale, or its average over all the map’s points. …which are, as I understand it, more in keeping with what cartographers compare by.
.
My unusual varied comparison-standards are due to the fact that scale matters, for close-examination, or distant-viewing. But I don’t think anyone other than me values all those comparison-standards that I value.
.
But we all agree that extreme shape-disproportion is undesirable.
.
You wrote:
.

The other thing is that I took Daniel Strebe's posting as an expression of a personal view, growing out of a situation where the term "shear" does not have a meaningful or consistent definition within cartography.

.
I don’t think that’s what he meant. But it’s certainly true that shear’s definition is less well-known. As I said, I’d assumed that shear was slant, until this thread’s initial article was posted.
.
But yes, as you suggest, the word “shear”, because of its different meaning for different people, might best be replaced by shape-disproportion or scale-variation, or angular-error.
.
There have been times here when I’ve found out that my usage of a word contradicts its standard meaning in cartography, or my term is different from a standard one, and I’ve adopted the standard term or meaning. …as with “shear” or “thematic-maps”, etc.
.
Anyway, I re-emphasize this:

Say that, starting at the equator, each tiny band of latitude is taken off a globe and laid on a table, each adjacent to the previous one. When they’re laid-out in a centered way, that gives you the Sinusoidal projection. Now, say you want to make that into Cylindrical-Equidistant, by increasing each parallel to fill the rectangle. You know that the higher lat bands are increased more than the lower-lat ones, because theyi start out shorter. That means that, on the right-hand side of the map, each band is sliding to the right, with respect to the band below it. …and on the left-hand side of the map, each band is sliding to the left, with respect to the band below it. Shear.
.
Now, for a different way of looking at it: Someone could argue:
.
What if you take a Mercator map, and then compress it NS. That doesn’t seem to be making shear. But are you sure? Before the compression, draw a diagonal line on the map. Make a dot almost on the line, above the line, and another dot directly across the line from it, almost on the line.
.
Now compress the map NS. Of course the line will become more nearly horizontal, and each dot will move NS toward the line. But that north or south motion of those dots isn’t perpendicular to the line. It has a component that’s parallel to the line.
.
The upper dot will say to the lower-dot: “You’ve moved to the right along this line!”. The other dot says, “No, you’ve moved to the right along this line.” Those two points, with respect to eachother, have experienced mutual displacement parallel to that line that is between them. Shear.
.
Michael Ossipoff
37 Sa
September 7th
1912 UTC

[quadibloc]

Thank you for this reply. It was entirely my mistake, then, to perceive a tone in your earlier comments to which I had taken exception.

When I had quoted my earlier post, I did it to give background, not to re-iterate anything to do with this subject, as I had made the point of interest to me: that the Transverse Mercator, like the Sinusoidal, could be considered "self-correcting", since the graticule of the projection reveals the exact degree of the exaggeration of size in the projection.

But if one admits that the Transverse Mercator is "self-correcting", so that slant is not the crucial factor in making a projection self-correcting, then if one can mentally tilt a quadrangle of latitude and longitude or mentally shrink and enlarge it, why can one not do anything that is necessary? And so any projection, regardless of its properties or lack of same, is self-correcting if it has a central meridian that is both conformal and uniform in scale:



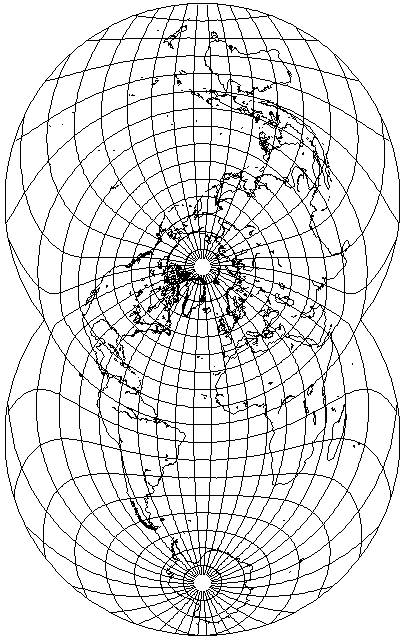
Even this example of a transverse Van der Grinten IV projection.

Maybe this is taking the notion too broadly. Or maybe this is a correct expression of the notion which I initially confined to the Sinusoidal and the Bonne's, but the property is not really a very useful or valuable one after all.

The idea being:

As the surface of the sphere cannot be reduced to the plane, every map distorts; this has long been known.

But perhaps there is a next best thing. Every map distorts, but perhaps some maps are so honest about their distortion that someone who looks at the map is still able to derive from the map an accurate mental picture of the globe.

The first example of this, and the most obvious, would be the Orthographic projection; it's a picture of the globe, so from looking at it, you see what the globe looks like.

Then I noticed how the Sinusoidal, with equal scale in two direction, makes its angular distortion very obvious and easy to reverse.

Having started thinking of the Transverse Mercator due to another thread, I thought - doesn't it also tell exactly what its error is? But if I admit it, isn't the presence of the central meridian as a reference really the only thing needed? Do I have any grounds on which I can say the Sinusoidal is more strongly self-correcting than these new examples?

[daan]

Daan pointed out that shear, angular error, shape-disproportion, deformation, are all different descriptions of the same thing, just numerically-different descriptions of the same thing… Which do I prefer? Shape-disproportion and scale-variation. They’re the same thing, of course.

This mightily confuses me.

I certainly did not explain that “shape-disproportion” means the same as angular deformation, given that I have never used the term “shape-disproportion”. It seems to be your contrivance, so I don’t know what it should mean, but it really does not sound anything like angular deformation. Proportion is tied intimately to the notion of ratios; disproportion ought to mean changes in relative sizes. But then you have thrown shape in front of it. To me, this ought to mean changes in the sizes of shape over finite regions (as opposed to infinitesimal, which is what angular deformation measures). And so, shape-disproportion, if there were such a term, which there is not, sounds to me like it ought to refer to how conformal maps (especially) change the shapes over large regions by virtue of their scale changes. This seems to be exactly the opposite of what you say.

Thus the hazard of inventing terms, especially when common, serviceable ones exist.

Similarly with “scale variation”: this term is commonly used when characterizing conformal maps, and is only clearly meaningful in that domain. That is because scale has no unambiguous meaning applied to non-conformal maps, even at a single point. So, exempting everything but conformal maps, scale variation means how that unambiguous scale varies across regions.

I prefer the term “angular deformation” to characterize the change in angles suffered by a point undergoing projection. I prefer the term “flation” to characterize the change in area measure suffered by a point undergoing projection. I prefer the term “interruption” to characterize separating points on the map that were adjacent on the spheroid. By avoiding the inclusion of “distortion” in the terms that describe these primary changes caused by projection, I strive to reinforce that each is independent of the others. This is in opposition to describing them as different facets of a single, more abstract category—a practice that I have seen corrupt people’s understanding of how they relate to each other.

I have no strong preference for terms talking about distortion across regions, other than “scale variation” for conformal maps. In other situations, I use descriptive verbiage at need.

— daan

[RogerOwens]

RogerOwens wrote:
.

Daan pointed out that shear, angular error, shape-disproportion, deformation, are all different descriptions of the same thing, just numerically-different descriptions of the same thing… Which do I prefer? Shape-disproportion and scale-variation. They’re the same thing, of course.

.
daan wrote:
.

I certainly did not explain that “shape-disproportion” means the same as angular deformation, given that I have never used the term “shape-disproportion”.

.
I didn’t write it as a direct quote. I was speaking conversationally, and, as such I made no claim that “shape-distortion” is a technical-term , or your name for, or my proposed name for a quantitative evaluation-measure.
.
As for the name of a quantative evaluation-measure, I’ve been saying “scale-disproportion”, or, more specifically, “min/max scale”. I prefer the latter. …even though it’s necessary to specify whether it refers to overall scale min and max over the whole map, or at some particular point on the map.
.
But yes, previously, probably earlier in this thread, I defined “Shape Accuracy”, abbreviated “ShAcc”, to refer to min/max scale at a point. It isn’t incorrect to coin that name for that meaning, as long as I explicitly define it so, as I did. At that time, I liked “Shape-Accuracy” because shape-problems were, then, to me, the most objectionable result of low min-max scale in equal-area maps. But, because low scale in any direction is disadvantageous for good measurement, or distant-viewing, I now prefer “min/max scale”.
.
As for my coining of terms, I’ll answer about that when I get to it below in your post.
.

It seems to be your contrivance

.
It wasn’t a contrivance. It was a casual conversational usage.
.

, so I don’t know what it should mean

.
I was conversationally referring to the deformation of local shapes (in small regions) resulting from low min/max scale at a point. I didn’t say it was a technical-term
.

Proportion is tied intimately to the notion of ratios; disproportion ought to mean changes in relative sizes.

.
Yes, and that’s why I now say “Scale-Disproportion” or “Min/Max Scale”.
.
I define “scale-disproportion” as “min/max Scale” at a point on the map. It would be better to always use one term, instead of two interchangeable ones, but “scale-disproportion” is a little shorter than “min-max scale at a point”.
.

But then you have thrown shape in front of it. To me, this ought to mean changes in the sizes of shape over finite regions (as opposed to infinitesimal, which is what angular deformation measures). And so, shape-disproportion, if there were such a term, which there is not, sounds to me like it ought to refer to how conformal maps (especially) change the shapes over large regions by virtue of their scale changes. This seems to be exactly the opposite of what you say.

Yes, shape-disproportion wouldn’t be a technical-term or a name for an evaluation-quantity, because even conformal maps don’t preserve shape over finite regions. Of course that’s obvious from a comparison of Canada’s shape on a Mercator, and on a globe.
.
Though I unambiguously defined “shape-accuracy” when I was using that term, of course it’s true that it isn’t a good term for a merit-quantification, because of its vague sound. I no longer use it.
.

Thus the hazard of inventing terms, especially when common, serviceable ones exist.

I wasn’t inventing a term. I was speaking conversationally. But yes, I do invent terms, when I want to measure for a quantity that others don’t measure for, or name something that there isn’t a term for, such as a projection-proposal, or an evaluation-quantity that no one else is interested in.
.
But, as I told Quadibloc, when I find out that there’s already a standard term for something that I’ve named differently, I adopt the standard term.
.
As for the different ways of stating the inaccuracies of equal-area maps, obviously there are various ways. Yes they’re numerically-different ways of measuring the same inaccuracy, in the sense that if one of those measures worsens, they all worsen together.
.
Because there are several ways of describing the inaccuracies of equal-area maps, then of course there’s no such thing as one standard term for it.
.
Average or max angular-error, overall min/max scale (same as greatest min/max scale at a point, on an equal-area map), average min/max scale over all the map’s points. Those are some of the measures that are used.
.
To those, I’d add average min-scale, over all the map’s points, divided by a reference-distance. …or min-scale over the entire map (out to North-Cape), divided by a reference-distance. Those are the measures that I prefer, for the quantitative-evaluation of an equal-area map.
.
No I’m not saying that everyone should adopt my favorite quantitative evaluation measures for equal-area maps.
.
Do I sometimes not use the standard term when there is one? If so, it isn’t intentional or stubborn. It’s just because I don’t know the standard term. When I find out about a standard term, I adopt it in subsequent usage.
.
When I say “a reference-distance”, I don’t mean to be vague. I mean, the map’s greatest X extent or Y extent …whichever of those map-dimensions is fit-critical for the available display-space. …whichever one limits the size of the map that can be mounted in the available display-space. When it isn’t known which of the map’s dimensions will be critical (maybe it isn’t known where it will be displayed), I suggest the geometric mean of the map’s X extent and its Y extent.
.
Of course the matter of whether the map’s X dimension or its Y dimension is fit-critical also depends on how you intend to orient the map on the wall. Speaking for myself, I like to orient the map so that (as nearly as possible, consistent with horizontal and vertical sheet-edges) north on the map is pointing toward actual north. But I realize that most people always mount a map with north at the top.
.
Or one could also choose the map orientation to make the best possible use of the available display-space. …by mounting the map with its shorter dimension (usually its Y dimension) aligned with the display-space’s limiting dimension.
.

Similarly with “scale variation”: this term is commonly used when characterizing conformal maps, and is only clearly meaningful in that domain.
.
That is because scale has no unambiguous meaning applied to non-conformal maps, even at a single point.

On a nonconformal map, it’s meaningful to speak of min and max scale at a point. In general, when scale-variation at a point is meant, that should be specified.
.
Whether a map is conformal or equal-area, the map’s scale-variation (over the entire map unless otherwise-qualified) means the same thing, and is a useful comparison. Of course, if the map is equal-area, then its greatest and least scales occur at the same point.
.
With the equal-area map, that scale-variation at a point results in scale-disproportion at that point on the map. But with both the equal-area and the conformal map, it’s overall scale-variation is relevant to how small the scale gets somewhere on the map, and is of interest for that reason. In that regard, yes scale-variation can meaningfully compare a conformal map to an equal-area map. ..though one usually wouldn’t.
.
For the scale-variation (overall max/ overall min scale) to be used to judge the how small the scale gets somewhere on the map, its scale-variation would be used along with its area (the square-root of its area, referred to some reference-distance such as the map’s greatest X-extent or Y-extent, or their geometric-mean).
.
That comparison can be made between any two maps, including a conformal map and an equal-area map. …though of course it’s more usual to compare two maps of same kind (conformal or equal-area).
.
Because I consider a map’s overall min-scale to be important, I prefer explicitly giving that, in terms of a reference-distance as described in the previous paragraph. I call that measure “min-scale”, and it’s my favorite quantative evaluation for an equal-area map. Because so many equal-area maps have a line-pole, resulting in zero point-min-scale at the pole, I define min-scale only out to the latitude of North-Cape (about lat 71.2).
.

So, exempting everything but conformal maps, scale variation means how that unambiguous scale varies across regions.

.
With any map, such as an equal-area map or a conformal map, it’s meaningful to speak of the min and max scales on the map, and their ratio. Overall min/max scale can compare a conformal map to an equal-area map, though such a comparison isn’t usually made, because of course one chooses whether one wants equal-area or conformality before one chooses the projection.
.

I prefer the term “angular deformation” to characterize the change in angles suffered by a point undergoing projection.

.
But you aren’t saying that it’s wrong to differently quantitatively-evaluate an equal-area map.
.

By avoiding the inclusion of “distortion” in the terms that describe these primary changes caused by projection, I strive to reinforce that each is independent of the others. This is in opposition to describing them as different facets of a single, more abstract category—a practice that I have seen corrupt people’s understanding of how they relate to each other.

Fair enough. But overall scale-variation (overall min/max scale) applies to and usefully compares all maps. (…though normally one has no reason to compare an equal-area map to a conformal map.)
.

I have no strong preference for terms talking about distortion across regions, other than “scale variation” for conformal maps. In other situations, I use descriptive verbiage at need.

.
Yes, for an equal-area map, which quantitative-evaluation one states depends on which seems more important for a particular comparison:
.
angular-error,
.
overall min/max scale
.
average point-min/max scale over all the map’s points
.
the map’s overall min-scale, out to lat 71.2, divided by a reference-distance
.
the average of the point-min-scale at all of the map’s points, divided by a reference-distance.

The square-root of the map's area, divided by a reference-distance.
.
The map’s space-efficiency (the % of the map’s circumscribing-rectangle that the map fills)
----------------------
Some of those measures can compare conformal maps to eachother, equal-area maps to eachother, or an equal-area map to a conformal map (something nearly never done, because one chooses equal-area or conformality before choosing the projection).
.
Michael Ossipoff
37 Su
September 8th
1634 UTC

[daan]

Because there are several ways of describing the inaccuracies of equal-area maps, then of course there’s no such thing as one standard term for it.

There is the phenomenon. There are ways to measure the phenomenon. You jumble them up. The standard terms for the phenomenon are angular deformation and angular distortion, so of course there are standard terms for it. There is also a standard way to measure the phenomenon (actually, two slight variants of each other). The name of the measure is ω. You use other measures. It is fine to use other measures if there is some purpose in doing so. Other measures do not affect the phenomenon or what it is, or ought to be, called.

On a nonconformal map, it’s meaningful to speak of min and max scale at a point. In general, when scale-variation at a point is meant, that should be specified.

Now you’re jumbling up a regional metric with a point metric. Scale variation is the change in scale factor across a region of a conformal map. It sounds like you wish to extend this notion to non-conformal maps, but when you describe what you mean by it here, you describe it as the variation in scale at a point, not a region. I have no idea how this is supposed to contribute to a regional metric or what meaning it could have in that context. I don’t even know what it means at a single point: Is it the maximum scale or the minimum scale or both or the ratio of the two, or what? And to what purpose? The minimum and maximum scale at a point is the semimajor and semiminor axes of the Tissot ellipse, denoted a and b. When I have occasion to refer to the minimal and maximal scale at a point, I use that symbology, or I write out “minimum and maximum scale”. Later you speak of “overall min/max”, but I don’t know how you intend to combine the point measures into an “overall” measure, and I seriously doubt the utility of doing so. On equal-area maps, doing so would tell me something or another, but the value of that information is much less than it is for a conformal map. For aphylactic maps, it would tell me even less.

— daan

[quadibloc]

The minimum and maximum scale at a point is the semimajor and semiminor axes of the Tissot ellipse, denoted a and b.

This finally inspired me to look up enough Tissot theory to find out that ω = 2 arcsin ((a - b)/(a + b)), so they're closely related.