All map projections distort. That is an inevitable consequence of the fact that the surface of the sphere, unlike that of the cone or the cylinder, is not reducible to the plane.
But I had thought: if we can't have a projection that doesn't distort, maybe we could have a next best thing - a projection that doesn't deceive. Although distortion is still present, perhaps in the right sort of projection, it might be obvious exactly what distortion was present, allowing the viewer of the map to easily deduce from the map what the globe looks like.
The most obvious case of this would be the Orthographic projection. After all, it's a picture of a globe, so to claim that from looking at it, one obtains a mental picture of how the continents would look on a globe doesn't seem too far-fetched.
But another possibility might be the Sinusoidal. Distortion is due to displacements in a single direction, parallel to the lines of latitude on the map; the way to correct any portion of a map, by straightening it up and making it vertical, is obvious. Everywhere.
Well, that might be sensible enough. But then it occurred to me that the Transverse Mercator might be considered self-correcting too:
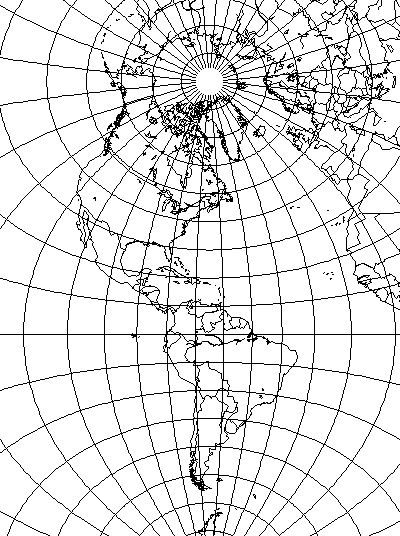
since one has the central meridian as a reference, so it's immediately visible by how much any quadrangle of latitude and longitude elsewhere on the map is enlarged - just compare it to a similar quadrangle on the central meridian.
But that opened the floodgates. Why require that the rest of the map, off the central meridian, either be equal-area, like the Sinusoidal, or conformal, like the Transverse Mercator? Couldn't the map reader mentally bend and twist into shape areas subject to both distortions?
The argument is logically plausible, and yet in these other cases, the map reader at least has to work harder. So maybe there is a "self-correcting" property, but it isn't all that useful in most cases, but perhaps with some hope of being useful in the simplest, strongest cases like the Sinusoidal.
After generalizing to a transverse Van der Grinten IV, though, I realized that the logic led one step further. If one can mentally distort a quadrangle of latitude and longitude to fit the correct shape shown in the central meridian, even if both shape and area are distorted, why does the central meridian even need to be part of the same projection?
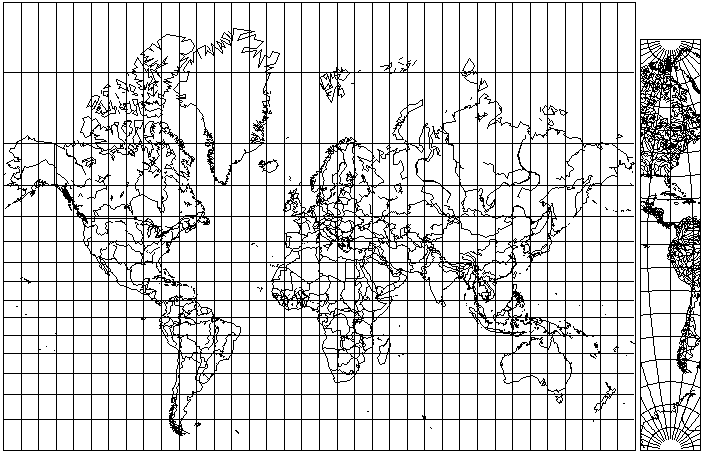
And so, voilà! An inset map, showing a minimal-distortion central meridian, lets the alert map-reader correct for the distortions of whatever projection is in use, and derive the true image of the globe from a map on just about any projection!
This seems to be the reductio ad absurdum that renders the concept of a "self-correcting" projection to be no more than nonsense. Or perhaps, even if it is far from a panacea, this kind of inset map actually is of some use. After having my logic run away with me to such a distance, I hardly feel qualified to venture an opinion.