History of the Oblique Hammer-Aitoff

[quadibloc]

I am not aware of any precursor to my “substitute deprojection” technique by which I constructed the Strebe 1995 projection.

In that case, I likely do not understand the technique you've used, and have confounded it with something trivial.

The technique I'm thinking of, although it may not have actually been used by Lagrange in coming up with the Lagrange projection, occurred to me immediately as the easiest way of explaining how that projection works to an unsophisticated reader. Take the world on a Mercator projection. Put it on another Mercator projection at twice the scale, with the Equators coinciding. Map that to the globe, and take the hemisphere your smaller Mercator is on, and project it with the equatorial case of the Stereographic.

And there you are - a conformal world in a circle.

And when Aitoff heard of Hammer's equal-area projection, he responded by devising this projection:



and, again, no doubt he just carried out the transformation mathematically without the need of a graphical conception, but I explained it as taking a cylindrical equal-area projection at nine-tenths of the scale, superimposing it on one at full scale, using the larger one to take the smaller one to a globe, and then projecting it from the globe to a Hammer projection, thus leading to a curved equal-area projection with pole lines.

[daan]

It’s fine to think of the conformal usages in terms of substitute deprojection—since they are instances of the technique—but I don’t think that’s how the originators conceptualized them. Moving on to the Wagner case, he found a way to generalize Aitoff’s meridional trick to parallels via a specific mathematical transformation, but again, I don’t think he conceived of that transformation in the general way of substitute deprojection. None of the papers written by him or Karl Siemon over many years alluded, in general terms, to planar transformations back-projected to the sphere before projecting forward again.

My innovation was to recognize that you could do something—map to plane, then pretend it’s a different projection when mapping back to the sphere, to then map back to the plane again—to “any” projection, and that doing this would preserve conformality when all projections involved were conformal, or equivalence when all projections involved were equivalent. This recognition of applicability to equal-area projections was particularly important to me. Conformal projections can be generated in endless profusion via any normal complex-valued functional composition. Equal-area projections, on the other hand, had been highly constrained until substitute deprojection. Das Umbeziffern was about as general as it got before then. I don’t think substitute deprojection’s property-conserving characteristics are completely obvious (except, perhaps, in hindsight): When Snyder and I communicated about my 1995 projection, he said he was able to prove to himself that it was equal-area, but confessed that the principle behind its development “astounded” him, and he was not quite able to grasp how it worked. I also would have expected others to have reported it much earlier if the principle were clear to them.

For a freely accessible description of the mathematics of das Umbeziffern (and substitute deprojection, and the even more interesting homotopy technique), see A bevy of area-preserving transforms for map projection designers. You will see how specific das Umbeziffern is and how little it evokes substitute deprojection.

— daan

[quadibloc]

I don’t think substitute deprojection’s property-conserving characteristics are completely obvious (except, perhaps, in hindsight): When Snyder and I communicated about my 1995 projection, he said he was able to prove to himself that it was equal-area, but confessed that the principle behind its development “astounded” him, and he was not quite able to grasp how it worked. I also would have expected others to have reported it much earlier if the principle were clear to them.

This is interesting. To me, explaining the Lagrange projection this way seemed so much more natural than going through the mathematical development, that I was sure that this was the best way to explain that projection to people who weren't sophisticated about mathematics in general or map projections in particular. If this technique is not as intuitive as it seems to me, and as your anecdote indicates, I may have to reconsider that.

At least my web page describing the Lagrange projection only dates from 2001, and is thus no threat to your priority.

[daan]

To me, explaining the Lagrange projection this way seemed so much more natural than going through the mathematical development, that I was sure that this was the best way to explain that projection to people who weren't sophisticated about mathematics in general or map projections in particular.

I quite agree. —Not that my opinion on the general digestibility of some concept means much; I seem to diverge from most people in how to think about a lot of things.

— daan

[quadibloc]

Not that my opinion on the general digestibility of some concept means much; I seem to diverge from most people in how to think about a lot of things.

In any case, based on your anecdote about Snyder, I've rushed to edit my page on the Lagrange conformal, in order to add a diagram to the page to supplement my verbal explanation of the procedure - if it's harder to understand than I realized, a diagram is needed.



Of course, though, you did recognize that the technique of substitute deprojection was valuable and significant, as well as applying it to produce new, potentially useful, equal-area projections. Even if many others, like myself, conceptualized projections like the Lagrange conformal in those terms, but viewed the technique as merely trivial, that does not alter the fact that you are rightly esteemed as its inventor - you are the one who showed it was useful, and gave it to the world.

[quadibloc]

I stick with Hammer.

Good for you. However, I've been looking into how pervasive the problems with the nomenclature of this projection have been.

I found that two rather authoritative sources - Down to Earth: Mapping for Everybody by David Greenhood, and the Natinal Geographic Society's The Round Earth on Flat Paper - named it for Aitoff, not mentioning Hammer at all. As they dated from 1942 and 1947, I wondered if the high feelings resulting from World War II had something to do with it.

But I Googled for more information, and came across the real explanation. The error, apparently, first appeared in the book Map Projections by David R. Hinks from 1912. In addition to mentioning this projection to many who may not have heard of it before, this is also the work that made people aware of Colonel Sir Charles Close's transverse Mollweide. So this particular error of nomenclature became deeply entrenched in the literature, causing a real danger of confusion.

I learned this from the paper Aitoff and Hammer: an Attempt at Clarification by John B. Leighly, Geographical Review v. 45, No. 2 (April 1955) pp. 246-249, it being online at Jstor.

[daan]

The error, apparently, first appeared in the book Map Projections by David R. Hinks from 1912.

Hincks lists Shrader’s atlas as using the “Aitoff” projection. Possibly Shrader misidentified it. Hammer himself shares some of the blame; he prominently credits Aitoff in both title and text of his paper.

Snyder conjectures that the misattribution was probably enhanced by mis- (or non-?) translation of Hammer’s paper, and credits the efforts of Leighly (1955) and Andrews (1952) for correcting the misattribution so vigorously that it is rarely found these days.

— daan

[quadibloc]

Hammer himself shares some of the blame; he prominently credits Aitoff in both title and text of his paper.

I'm not sure if you can call that blame; Aitoff had the original idea, and Hammer just suggested applying it where it would be more useful. But certainly a language barrier does not help.

[daan]

Hammer just suggested applying it where it would be more useful.

Hammer recognized that the practice preserves differential areas. That turned the technique from “huh, cute” to important.

— daan

[quadibloc]

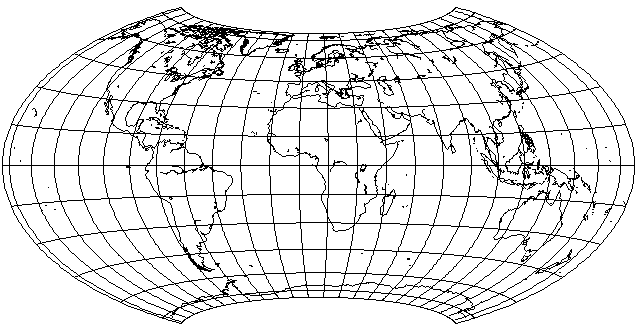
Hammer recognized that the practice preserves differential areas. That turned the technique from “huh, cute” to important.

Oh, that's true. Still, given that Aitoff's invention was recognized as original and valuable in Germany at the time, for Hammer to wish to appear not to be trying to steal credit for someone else's invention is not unreasonable. So he titles his paper something like "An Equal-Area version of Aitoff's projection", explains his idea in a paper of which he is the author, without feeling the need to mention personalities once in the paper... because he is confident that readers of the paper will realize that he published this paper about an idea, small though it may be, of his own, rather than being called upon by Aitoff to report Aitoff's new brainstorm in the literature.

And it would have worked, and, indeed, it did work, in the German-speaking world (speaking of oneself in the first person, rather than as "the author" is not the custom in the scientific literature and so on)... but in the English-speaking world, his paper was seen by someone who apparently didn't understand much German, and also apparently thought the German scientific community was made up of incomprehensible aliens who publish papers for each other; possibly a hive mind.

Hammer didn't toot his own horn because a scientific journal is not the place for that sort of thing; I can't blame him for what is a shocking breach of academic standards through carelessness by one individual in the English-speaking world - whoever he may be - that went unchecked for so long. Of course, _these days_, if someone is so daring as to publish a scientific paper in German, one will usually include an English-language abstract, but back in the 19th Century, the overwhelming dominance of the United States in the industrialized world was not quite what it became after World War II.

What is mysterious to me is what people failed to think of that didn't require a knowledge of foreign languages. The same 1912 book which introduced Hammer's projection to the English-speaking world in 1912 also exhibited a transverse aspect of the Mollweide. Yet, apparently, it took until 1942 before someone thought a transverse aspect of Hammer's projection was worth doing.

Of course, transverse and oblique aspects of projections require a lot of calculation. And the Mollweide projection, being pseudocylindrical, required less calculation than the Hammer. Seeking an optimal distribution of error for an oblique aspect... just may not have been felt to be worth the effort. As well, comparing Bartholemew's Nordic to a similarly obliqued Mollweide, the former puts Britain and continental Europe in an area with lower error, but the latter may have smaller area for the United States, so perhaps the Mollweide was actually regarded as better balanced.

In 1948, Bartholomew wouldn't have had a desktop computer, he wouldn't even have had the opportunity to run out and buy an SR-59 pocket calculator with magnetic cards (like John P. Snyder, of course). But still, things had changed since 1912. So the question that now besets me is: did Bartholomew make use of, say, IBM electronic tab equipment (mechanical equipment by Powers-Samas, somewhat more common in the United Kingdom, wouldn't have been flexible enough) to assist him in the required calculations for these projectins? (Even Flattening the Earth, of which my copy has arrived, answers this not.)