I think I can, although I admit I'm a bit intimidated by your expertise in the field, as it's far greater than mine.daan wrote:Adams does not address the octahedral case in Elliptic Functions Applied to Conformal World Maps (1925). I know Cahill credits Adams for his conformal butterfly’s mathematical development, but I don’t find any publication that obviously contains that. Adams published Conformal Projection of a Sphere Within a Square in 1929. That’s one I don’t have that, but the title doesn’t suggest it would be in there, and Snyder does not note a publication for Adams’s octahedral development, either.
So… I’m skeptical. But, perhaps you can enlighten us.
Basically, pull the same trick that turns the Stereographic projection into this:
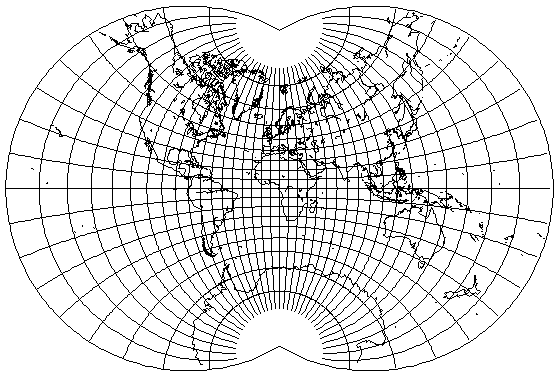
but instead of using the Stereographic, start from this projection in Elliptic Functions Applied to Conformal World Maps (1925):
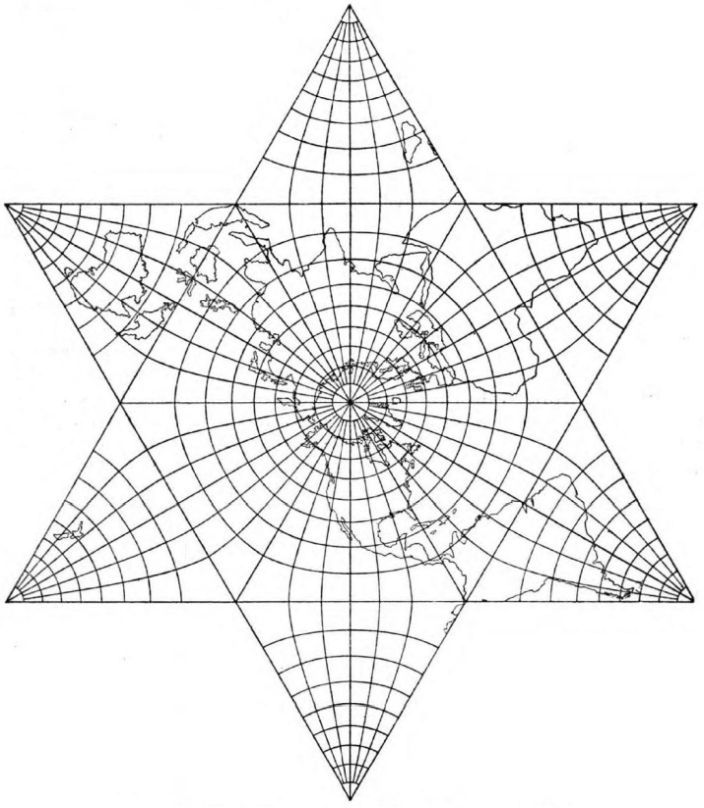
and, bingo, you're just using four of the six points of the star and that's your octahedron. If I didn't have the polynomial for the six-pointed star from Adams' book, and if the transform to the octahedral case weren't trivial like this, I would never have harbored hopes of someday implementing it.
