Eckert IV vs Eckert VI. Other related topics.

[RogerOwens]

At the end of my post before this one, I accidentally said that I swear that the only additional projection that I'll ask you to post an image of will be "Cylindrical Equal-Area with reciprocal EW/NS scale disproportion at (lat 45, lon 0) and the equator", when I meant to say "Equal-Area PF8.32 with reciprocal EW/NS scale-disproportion at (lat 45, lon 0) and the equator".

(I've now corrected that error in an edit, but I felt that I should still mention it in a separate post.)

Of course, I've already requested both cylindricals, in the post before this one. I greatly appreciate your help with that, and, as I said, I guarantee that the only remaining one that I'll ask for will later be Equal-Area PF8.32

Michael Ossipoff

[Atarimaster]

Cylindrical equidistant:


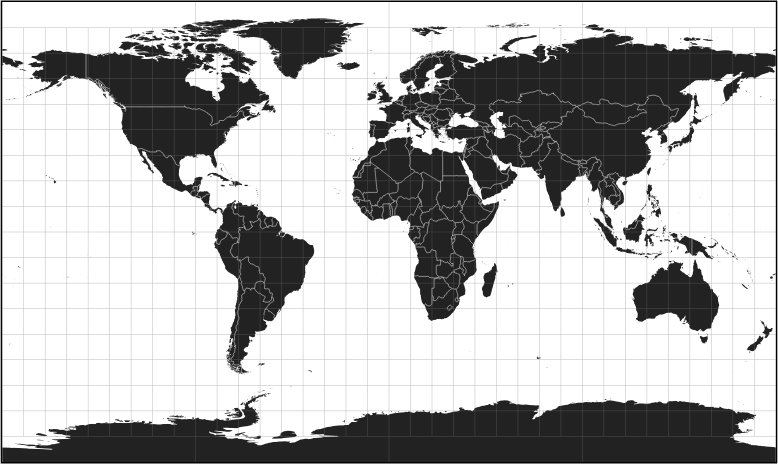
Cylindrical equal-area:



btw, standard parallels are approximately 32° for the cylindrical equidistant and 24° for the cylindrical equal-area.

[RogerOwens]

Tobias--

Thanks for posting those two cylindrical images.

The Cylindrical Equidistant one, for Europe, the U.S. and Africa, looks good, and a lot like Equidistant PF8.32 with the same latitudes-compromise, because Equidistant PF8.32's meridians are nearly straight and vertical up to European and North-American latitudes.

The Cylindrical Equidistant of course can't treat the Arctic as well as Equidistant PF8.32, and the Cylindrical's Svalbard is significantly flattened. ...but not unrecognizably so, as it is in most Cylindrical Equal-Area maps. But the more perfect shape for Svalbard is an advantage that PF8.32 brings.

Svalbard is what I use to judge arctic shape, because it's the highest-latitude piece of land that's big enough for its shape to be clear on a world map. I guess the shape of the Franz-Josef Land island-group could be used too.

As for the Cylindrical Equal-Area, i posted the wrong compression-factor. Sorry about that.

What I forgot was that, where a Cylindrical Equidistant conformal at the equator flattens a place by a factor equal to the cosine of its latitude, the Cylindrical Equal-Area flattens it by a factor equal to the square of the cosine of its latitude.

So, for the Cylindrical Equal-Area, the horizontal compression factor should have been .7071 instead of .8409. (The desired compression-factor is the square-root of the factor by which the map would flatten a place at (lat 45, lon 0) when the map is conformal at the equator).

So, due to my error about the compression-factor, that Cylindrical-Equal-Area map flattens Europe and North-America more than it should.

I choose the compromise between latitudes 45 and 0, but the familiar already-proposed Cylindrical Equal-Area conformal at lat 30 has a good justification too: As I was mentioning before, half of the Earth's surface has latitude less than 30. So that map conformal at lat 30 is conformal right at the boundary of the -30 to +30 band that consists of half of the Earth's surface.

So that familiar Cylindrical Equal-Area conformal at lat 30 has a good worldwide optimization justification.

I doubt that there's any better worldwide optimization than that. What are some other possibilities that could be considered?

One could at first consider a MinMax optimization for scale-disproportion, but that wouldn't work, because a cylindrical's scale-disproportion is infinite at the pole. One could at first consider minimizing the root-mean-square sum of the scale-disproportion over the entire Earth. But that would heavily favor the Arctic, or maybe even polar, regions, because of their very great scale-disproportion on a cylindrical map. That's my objection to the root-mean-square optimizations.

Anyway, sorry to have posted the wrong compression-factor for the Cylindrical Equal-Area. It should have been .7071 instead of .8409, for the Cylindrical Equal-Area map. (But .8409 was right for the Cylindrical-Equidistant map.)

Michael

[RogerOwens]

Another interesting possibility:

What if the worldwide optimization of conformality at lat 30 were used in the Cylindrical Equidistant map?

To achieve that, .866025 is substituted for .8402, as the horizontal compression factor, in the formula for x.

Michael

[Atarimaster]

Michael,

since I got a little confused about which values you wanted and since I found it interesting to play with the values of your linear power-function projections, I set up a little tool (again, the implementation was done a bit quick & dirty):
http://tobiasjung.name/mop/mo-projections.php

Usage should be quite self-explanatory:
Input values for the projection you want to render (power function or equal-area or equidistant) and hit the corresponding "Render projection" button.
There’s no input validation whatsoever, so if you enter an inappropriate value (or e.g. some text instead of a numerical value), no image will be rendered.

You can download current projection as SVG file.
File name will be "projection_", followed by a shortcut indicating the kind of projection you’ve selected (pf or ea or ed), followed by the values you’ve entered, so the image will be saved as, for example, projection_pf_3_0.808122036.svg, projection_ea_0.7071.svg etc.

This tool is meant to be a temporary solution. Rest assured that I will not publish the link anywhere else and that I will remove it again sometime soon.

Regards,
Tobias

[RogerOwens]

Hi Tobias--

Thanks for that map-projection computation-tool. I'll give it a try.

But I have to admit: I feel about computer tools, apps, utilities, files, etc., the same way you feel about mathematics.

So it's better if someone who knows computers, files, etc., as you do, does the computer-imaging--something that I fully admit that I'm completely unqualified for.

I want to assure you that these image-requests won't go on indefinitely. There are only these few projections that I'm proposing:

Cylindrical Equidistant, Cylindrical Equal-Area, and Linear PF8.32--all 1) conformal at lat 30, and 2) also with equal and opposite scale-disproportion at (lat 45, lon 0) and along the equator.

I haven't yet written the formulas for Equal-Area PF8.32 with those same two shapes-configurations.

But yes, as you mentioned, I've proposed and requested images of so many versions, that it's becoming unclear what additional images I'm requesting.

Because I've proposed so many versions, let me summarize them here, starting with the Cylindrical projections:

--------------------------------------------------------------------------------------
1. Cylindrical Equidistant, with scale-disproportion equal and opposite at latitudes 45 and 0.

Horizontal compression-factor in the formula for X: .8409

(image already posted)
----------------------------------------------------------------------------------------
2. Cylindrical Equidistant, conformal at lat 30.

Horizontal compression factor in the formula for X: .866025

(image requested)
----------------------------------------------------------------------------------
3. Cylindrical Equal-Area with scale disproportion equal and opposite at latitudes 45 and 0

Horizontal compression factor in the formula for X: .7071

(image requested)
----------------------------------------------------------------------------------
Cylindrical Equal-Area conformal at lat 30

Horizontal Compression-factor in the formula for X: .75

(This is a familiar already-proposed version of Cylindrical Equal-Area, but a posted image would be good, for completeness)
------------------------------------------------------------------------------------
Linear PF8.32, with scale-disproportion equal and opposite at (lat 45, lon 0) and at equator.

Horizontal compression-factor in the formula for X: .842215

(image already posted)
------------------------------------------------------------------------------------

Linear PF8.32 conformal at lat 30

Horizontal compression-factor in the formula for X: .86612

(image requested)

---------------------------------------------------------------------------------------

Equal-Area PF8.32, with scale-disproportion equal and opposite at (lat 45, lon 0) and at equator

(formulas not written yet)
-------------------------------------------------------------------------------------------

Equal-Area PF8.32, conformal at lat 30

(formulas not written yet)

----------------------------------------------------------------------------------------------

Michael

[RogerOwens]

Topics in this post:

1. Cylindrical Equal-Area, with 45/0 compromise.
2. Four Grafted maps (Cylindrical + Sinusoidal)
...(I won’t ask for images of them)
3. Explanation of the Purposes and Justifications for my proposals:
-------------------------------------------------------

1. Cylindrical Equal-Area, with 45/0 compromise:

There’s already a good, already-proposed, Cylindrical Equal-Area (CEA) map: The one that’s conformal at latitude
30.

Because lat 30 is right on the boundary of the -30 to +30 belt that encompasses half of the Earth’s surface, this version qualifies best as a worldwide compromise.

Its scale-disproportion for the U.S. and Europe, and for Africa, isn’t excessive.

Having always resided in the U.S., I’m particularly familiar with its expected shape on a map. Surely that’s true of others, regarding the shape of the country where they reside.

Of course I and the other two people at this forum reside in mid-latitudes, and so any scale-disproportion in that region might be the most objectionable to its residents. Of course differently-scale-proportioned versions of a map could be chosen and used in different latitudes, just as different central-meridians are used in places at different longitudes.

Therefore, at this forum, I offer my 45/0 compromise version of Cylindrical Equal-Area. It’s intended as a direct compromise between equatorial and middle latitude.

It will reduce (in comparison to the conformal at lat 30 version) the horizontal dimension of countries (including the U.S. and Germany) by a factor of .9428, thereby reducing those countries’ north-south flattening in the map, thereby improving the appearance in the map, of countries that are north-south flattened in a CEA map.

That’s why 45/0 CEA is one of the maps whose image I request, in my previous posting.

Six Grafted Maps (Cylindrical and Sinusoidal):

Already proposed is a graft of Mercator and Sinusoidal, at lat 45. I propose 6 other grafts of Cylindrical and Sinusoidal maps:

Conformal:

1. Mercator with Sinusoidal grafted to it at the Arctic Circle

2. Mercator with Sinusoidal grafted to it at lat 70

(…in order to include more of the inhabited land in Mercator, copying from a Russian graft of Mercator
…and Cylindrical-Equidistant at lat 70.)

Equidistant:

3. Cylindrical-Equidistant grafted to Sinusoidal at a latitude chosen to give the map the same space-efficiency as Eckert III, Eckert IV and PF8.32

...with the CE map scale-proportioned for conformality at lat 30

4. Cylindrical-Equidistant grafted to Sinusoidal at a latitude chosen to give the map the same space-efficiency as Eckert III, Eckert IV and PF8.32

…with the CE map scale-proportioned for equal and opposite EW/NS scale-disproportion at latitudes 45 and 0.

Equal-Area:

5. Cylindrical-Equal-Area Grafted to Sinusoidal at a latitude chosen to give the map the same space-efficiency as Eckert III, Eckert IV, and PF8.32

…with the CEA map scale-proportioned for conformality at lat 30

6. Cylindrical Equl-Area Grafted to Sinusoidal at a latitude chosen to give the map the same space-efficiency as Eckert III, Eckert IV, and PF8.32

…with the CEA map scale-proportioned for equal and opposite EW/NS scale-disproportion at latitudes 45 and 0.
----------------------------------------------------------------------------------

I haven’t seen most of these grafted maps, or calculated their scale-disproportions in comparison to those of their PF8.32 counterparts, but I like the equal-area versions for their easier explanations (easier explanation of the specifics of their achievement of equal-area), in comparison to their PF8.32 counterparts. To me, easy explanation is an important consideration for a map-projection proposed for public use.

I’ll later post more specific definitions of these proposals, including their graft-latitudes and their formulas.

…without requesting images of them.

Formulas for Equal-Area Pf8.32 will be posted as well.
------------------------------------------------------------------------------
Explanation of Purposes and Justifications for My Proposals:

Cylindroid Maps:

I don’t claim that everyone should agree with my map-preferences. It’s an individual matter.

Pseudocylindrical maps, and Cylindrical maps more-so, have some important, useful, valuable properties, and I (speaking for myself), want those properties in a world map.

I offer and propose various Cylindroid (Cylindrical and Pseudocylindrical) maps, in case other people consider their properties useful, for at least some applications.

Space-Efficiency:

I don’t claim that space-efficiency should over-rule all other considerations. But I claim that it’s desirable, and that there’s a good case for maximizing it when other desired properties or considerations don’t conflict with it.

High space-efficiency means that, for a given rectangular area-availability, the map, and (some or all of) its portrayed places, are shown larger. That can only be a good thing.

More detail can be shown.

The map can be used at a greater distance (in a classroom, for example).

Just easier and more convenient to use.

These considerations become even more important for thematic maps, particularly those with more than one theme (showing more than one thing’s geographic distribution).

Anyway, in general, all else being equal, when there are no conflicting considerations, isn’t a bigger map better, for a given available rectangular space?

For equal-area in particular:

The Sinusoidal has advantages and good reasons to choose it (as do the similarly-shaped Parabolic Equal-Area and Quartic-Authalic).

But, though some kinds of thematic maps need equal area to show what they’re intended to show, there’s another reason to choose equal-area:

Fairness to everyone using the map to look at different parts of the Earth.

It could rightly be argued that a map’s total area should be divided in fair proportion among all places, to achieve that fairness.

But, by the same motivation, then, doesn’t that also call for the whole map’s area, which we want to be fairly divided, being large, so that everyone’s share of it will be larger?

If you want a fair share, a justly-large share, then you’ll want the area being shared to be large too, so that your share will be larger.

Whether the area of your place-of-interest is smaller because of it not getting its proportionate share, or because the whole map is small—Either way your share is smaller.

And furthermore, that consideration can obviously be extended to maps that aren’t equal-area.

PF8.32 and the Cylindrical/Sinusoidal grafts:

Of course high space-efficiency can be over-ruled if it conflicts with other desired considerations.

The main alleged “problem”:

Looking at some high-space-efficiency linear or equal-area maps, one could get the false impression that, for linear or (especially) equal-area world maps, high space-efficiency is incompatible with good scale-proportion everywhere.

For example, look at Cylindrical Equal-Area, conformal at lat 45, or Eckert IV. Africa is considerably skinny. Likewise, some object to the flattening of the U.S. and Europe in Eckert III, and in Cylindrical Equidistant conformal at the equator, or the skinnying of Africa in Cylindrical Equidistant conformal at lat 45.

That false impression, that unnecessary “problem” is the result of an unfortunate choice of standard-parallel.

Look at Cylindrical Equal-Area (CEA) conformal at lat 30. Scale-disproportion isn’t unacceptable for the U.S., Europe, or Africa.

(As described above, CEA with equal and opposite scale-disproportion at latitudes 45 and 0 will give better shapes for the U.S. and Europe, if that’s what is more desired by residents of those regions.)

Yes, the Arctic is significantl flattened. …admittedly unavoidable in CEA. That flattening is also significant, but not to unrecognizability, in Cylindrical Equidistant.

That’s where Equal-Area PF8.32, and the various Cylindrical/Sinusoidal grafts come in. In low and middle latitudes, it’s virtually identical to CEA, because its meridians don’t significantly curve until higher latitudes. But its point-pole gives a much more realistic Arctic, without the extreme Arctic flattening of CEA.

So I suggest that Equal-Area PF8.32 is the high-space-efficiency map that, even with equal-area, doesn't have excessive, objectionable or problematic scale-disproportion anywhere.

Of course that advantage will be shared, as well, by grafts of CEA and Sinusoidal, defined above in this post.

Of course Linear PF8.32, and the Cylindrical-Equidistant/Sinusoidal grafts, will bring the same improvement with respect to Cylindrical Equidistant maps—though, for equidistant maps, that improvement isn’t as greatly needed.

I’ll post specific definitions for my proposed grafts of Cylindrical and Sinusoidal maps, specifying their graft-latitudes.
I’ll post tables of scale-disproportion at selected places of interest, for my Equal-Area PF832 versions, and for the various Cylindrical/Sinusoidal grafts that I propose.

The places of interest will be:

The center of Africa
The center of the U.S.
The center of Germany
Svalbard
Franz-Josef Land

Michael Ossipoff

[Atarimaster]

I’ll just link to the requested images now…

2. Cylindrical Equidistant, conformal at lat 30.
Horizontal compression factor in the formula for X: .866025

http://tobiasjung.name/mop/mo-projectio ... f=0.866025

3. Cylindrical Equal-Area with scale disproportion equal and opposite at latitudes 45 and 0
Horizontal compression factor in the formula for X: .7071

http://tobiasjung.name/mop/mo-projectio ... a&f=0.7071

Cylindrical Equal-Area conformal at lat 30
Horizontal Compression-factor in the formula for X: .75
(This is a familiar already-proposed version of Cylindrical Equal-Area, but a posted image would be good, for completeness)

http://tobiasjung.name/mop/mo-projectio ... rea&f=0.75

(And I think there’s no harm in stating that the »familiar already-proposed version« is the Behrmann equal-area…)

Linear PF8.32 conformal at lat 30
Horizontal compression-factor in the formula for X: .86612

http://tobiasjung.name/mop/mo-projectio ... &f=0.86612

[RogerOwens]

Tobias--

Thanks for the links to those additional images !

Is it alright if I display those images at this forum, so that they're immediately-visible to visitors to the forum? That would make them available for visitors to look at more quickly and easily.

More important, when the set of images are posted in one posting here, it's quick and easy to scroll from one to another, for quick and easy comparison. I've been comparing, in that manner, the images that you posted, and it's really convenient, and best reveals the projections' differences.
------------------------------------
February 15 Edit:

The comparisons with Gall Stereographic that were previously at this place in this post were incorrect. Any CEA has a really big arctic scale-disproportion problem. With CEA, you really have to write-off the realistic appearance of the arctic--good for judging the sizes of arctic places, but not for showing what they look like.

But I feel that, with few exceptions, world maps should be conformal, linear or equal-area. Though it could sometimes be desirable combine equal-area with the advantages of a cylindrical, it seems usually better to show the Arctic better, which, if a large (for a given horizontal-space) equal-area map is desired, is a good reason for Equal-Area PF8.32 or a CEA/Sinusoidal graft.
------------------------------------

So is it alright if I post the images to display at this forum?


Michael

[Atarimaster]

So is it alright if I post the images to display at this forum?

Yes.

Since they are based on your formulae and the d3.js scripts, I see no reason to raise a claim on them.
Therefore, you and anyone else can copy, modify and distribute them without any restrictions.