Questions about optmization for equal-area world maps

[daan]

You only have one degree of freedom: the latitude of the joint which, if you fix at Bartholomew’s choice, leaves you zero. You don’t get a second standard parallel because doing so changes the cone constant such that the joint no longer follows the same arc on the plane as Bonne. I see now that this won’t meet your needs because Albers, with two standard parallels at that low of a latitude, looks more like a bent cylindric projection than a conic, having a very different cone constant from the Bartholomew equidistant. You could use Bartholomew’s standard parallels and shrink the Bonne a little or expand the Albers a little in order to get the joint to line up, but that would defeat the point of using an equal-area northern section.

— daan

[quadibloc]

ou don’t get a second standard parallel because doing so changes the cone constant such that the joint no longer follows the same arc on the plane as Bonne.

That objection applies with equal force to the Simple Conic. Bartholomew's Regional Projection uses a simple conic with standard parallels at 23.5 degrees and 66.5 degrees. The sections adjoined to it are on the Bonne projection, but they're not Bonne's projections with standard parallels of 23.5 degrees in the south and 66.5 degrees in the north, respectively - the standard parallels aren't even computed, the arcs from the conic are just taken, with true distances measured out along them.
I do have, on my page, an example of joining a conic projection to a Bonne projection where both have one standard parallel, and are joined along it, the northern part being on the conformal conic:

so I was myself thinking at one point of projections that met the condition you are applying here (I had to hold my nose a bit to cover the Bartholomew Regional despite liking it a lot, as I strongly disapprove of kinks in general, i.e. the Goode Homolosine.)
It wasn't just being leery of the mathematics, though, that had me not using Albers. Bonne by itself ought to give me enough flexibility, I had thought, also, it wasn't clear that the purposes for which a projection like the Regional would be desired are purposes that also benefit from true equal-area.

[daan]

I didn’t quite follow all that, but to be clear, Bonne has only one standard parallel. The premise of the amulet projection is to join the Albers and Bonne where they have identical geometry, which is where Bonne’s single standard parallel and Albers’s two parallels are all set to be the same. Hence, equal-area throughout, and no kinks. (That is, the first-order derivatives are the same, but of course higher order derivatives are not; whether this concerns you or not depends on whether æsthetics or analytics are your “first order” priority.) It’s then the same project to interrupt the amulet as to interrupt Bartholomew’s—but actually easier, because the joint is perfect and there is no kink to iron out (as Bartholomew did) or leave as an eyesore (as Jason Davies did).

If we give the northern section the same cone constant as Bartholomew’s, we have cone constant n that gives standard parallels of 43.6799°, close to the 45° of the illustrations on Geocart’s site. However, the pole arc is much larger than Bartholomew’s, and, more impactfully, the latitude of the join is way up there instead of at 23.5°. This relegates more of the map to Bonne, thereby deepening the interruptions, which tears into central Asia. (Bartholomew’s trick for the Indian subcontinent would mitigate some.) Roughing it out (click on image to expand it):

Albers+Bonne, Bartholomew’s arrangement, joint parallel = 43.6799°

Barts.jpg (191.63 KiB) Viewed 1649 times

Meanwhile, if we set the standard parallels way down at 23.5° to keep the length of the interruptions the same (and again avoid the kink), we get a massive pole line with a northern section that looks more like a bent Lambert cylindric than any sort of conic. Not pleasing.

— daan

[quadibloc]

I didn’t quite follow all that, but to be clear, Bonne has only one standard parallel.

Oh, absolutely.

I may have been mistaken in thinking you had made a mistake, I could have misunderstood what you were talking about.

Basically, what you were saying is absolutely correct, and the projection you exhibited would be what is required, if the condition is imposed that there be no "kinks" in the resulting projection.

But while the projection was fudged in the Times version to hide the kink - a small band was neither conic nor Bonne's - Bartholomew's Regional Projection did have a kink. And when I was saying I could use Albers, I meant subject to accepting that a kink is allowed in the resulting projection.

Bartholomew's Regional Projection used a Simple Conic with two standard parallels. The Bonne's projections that adjoined it did not have their standard parallels at the place they joined up, so the meridians hit the standard parallel of the conic at an angle. Thus, there was a kink. The Simple Conic has the same problem that you identified as preventing the use of Albers' Equal-Area Conic, both conic projections are in the same situation, to do what Bartholomew did, you have to accept the compromises that he did.

So your example without a kink of a Bonne's joining up with an Albers at their mutual standard parallel without a kink embodies the same principle as my example of a Bonne's joining up with a Lambert at their mutual standard parallel without a kink. So I think we're on the same wavelength here, and I understand you, and if I wasn't clear before, I hope you understand me now.

[daan]

Yup. All is clear. Thanks.

— daan

[daan]

Since you seem to have resigned yourself to the kink, a way to make this equal-area version work is to use Lambert equal-area conic (= Albers with one standard parallel at north pole) and set the Lambert’s standard parallel to 23.5°N. This gives the meridians the proper spacing to line up with the Bonne, whose standard parallel needs to be solved for to give the same circular arc at the joint. It’s about 48.5°. Roughed in:

Bonne, standard parallel = 48.5; Lambert equal-area conic, standard parallel = 23.5.

Barts2.jpg (194.63 KiB) Viewed 1646 times

This gives equal-area throughout, gives a pointed pole, and in general suffers little drawback compared to Bartholomew’s construction.

— daan

[quadibloc]

This gives equal-area throughout, gives a pointed pole, and in general suffers little drawback compared to Bartholomew’s construction.

True, except for the fact that the region with Albers' equal-area projection is quite stretched. Thus, I would have chosen somewhat different standard parallels for the Albers.

As for what to do north of the standard parallel, one can either tolerate considerable horizontal stretching for just the Arctic - or use the Bonne's again in the north with another kink, like Bartholomew did, but rather than too many interruptions (like the Kite) or too few (like the first Regional) just interrupt into two lobes in the Arctic.

I'm not fully reconciled to the kink, I simply admit it's needed for a projection like Bartholomew's. But I haven't found something different that works nearly as well; so if I want to avoid a kink, the best I currently have is just interrupted Bonne's.

[quadibloc]

Turning from heavily interrupted projections like Bartholomew's Regional Projection to uninterrupted equal-area projections, I was quite impressed by the Strebe Asymmetric projection. Making the Southern Hemisphere, where the major continental groups don't extend as far poleward as in the Northern Hemisphere, more like a cylindrical equal-area projection makes good sense.

Since G.Projector handles the Strebe 1995 projection, I managed to add an illustration of it, and a brief mention of it, to my web site. I'm afraid, though, that I couldn't quite see exactly how the mapping from Eckert IV to Mollweide to the globe and back to the Hammer-Aitoff was carried out, since the poles on Strebe 1995 were too curved to correspond to any parallels on the Hammer-Aitoff. (I suppose I could have just followed the equations, but if I don't understand the equations, debugging the program is much harder if anything isn't perfect. My code uses different scaling factors for angles, among other things.)

But I could only mention the Strebe Asymmetric. However, while I couldn't actually illustrate it, I was able to illustrate the principle:



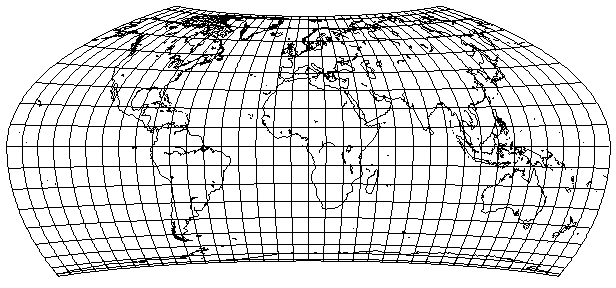
as, if one isn't worried about having rounded corners, one can do the same sort of thing with the more limited toolkit that was used to come up with the Wagner VII projection. Longitude is mapped to 120 degrees, exactly like the Wagner VII. The extra vertical stretch is only 8%, milder than in the Wagner VII. The only parameter that differs between top and bottom is the sine-to-sine scaling; 92%, instead of 90.6% as in the Wagner VII, for the Northern hemisphere, to get an even shorter pole-line... and 60% in the Southern hemisphere, from whence comes the asymmetry.

Also, I've attempted to do a better job of reverse-engineering the Denoyer semi-elliptical projection than what I've seen in most mapping programs: my result was this:



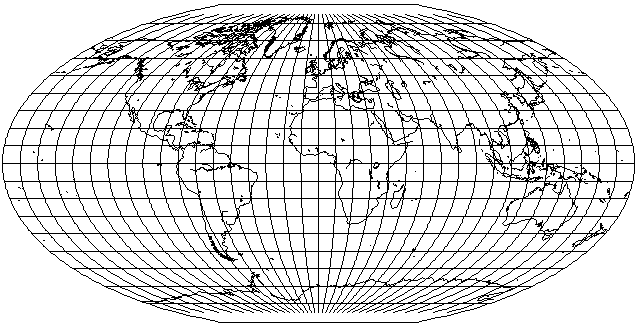
I felt existing attempts to imitate that projection made it look like the Ortelius Oval: my attempt may have made the degree to which meridians come closer nearer the central meridian as you approach the poles perhaps a little too gentle.

[daan]

Nice job on that Wagner VII. A lot of people don’t care for asymmetry in a projection, but I think it’s preferable to interruption, and as such, is the only way to selectively improve a globe having asymmetrical distribution of regions targeted for lower distortion.

[Edited; my first explanation was confused.] What’s going on with the Strebe pole line is that the effect of the Hammer curvature gets applied to a different parallel on the shrunken Eckert, and the curvature is not only upward, but inward (because that is the vector field of the Mollweide-to-Hammer transformation). And then that effect gets magnified when the full scale is restored.

I don’t have a useful copy of an original Denoyer map to compare against. I think everybody but you uses Snyder’s recreation. I’m confused by your description of Snyder’s as looking like Ortelius oval though: If anything, I’d say yours is more in the direction of Ortelius, but neither is close.

— daan

[quadibloc]

Nice job on that Wagner VII.

Thank you. This was just a first cut, though, to demonstrate the principle. The Northern Hemisphere isn't optimized; maybe it should have a pole line that's a bit wider, and maybe the projection as a whole should have a little more vertical stretching to have less total area. At the moment, though, I don't think I'll be worrying about that.

I’m confused by your description of Snyder’s as looking like Ortelius oval though:

I'm referring to one specific thing, but I'm not sure how to explain it. This message board does not have the ability to display an image from a file, only an URL.

For now, I'll use words. When I create a map using G.Projector in the Denoyer Semi-Elliptical projection, and I believe it's using Snyder's recreation like everyone else, at the North Pole line, the meridians for 10 degrees east and west of the central meridian touch the central meridian at the pole line. That's what reminds me of the Ortelius Oval. I don't have an old school map on the Denoyer Semi-Elliptical Projection handy myself, but even from photos for such things as eBay sales - and I've actually found three that are a bit better than that - I can tell that they don't touch in the center at the pole line. They are closer, with the meridians at the edge of the projection being about eight times as far apart as the ones in the center, but the ones in the center don't touch.

That's why I tried to make my own recreation of that projection which avoids the flaw. However, in other respects, over much of the area of the map, it may still be less accurate than Snyder's.

There's another thing I've been up to. The Dietrich-Kitada projection does seem to be good over quite a large area of the map, but it's also very bad over a large area of the map. This makes it a challenge to avoid the problem areas. I had tried several different aspects of the projection, and it seemed like nothing would work for a world map. But when I tried the aspect used for the Nordic projection, while that didn't quite work as is either, it definitely gave hints as to how it might be possible to proceed. This projection is still not great for Australia, New Zealand, and South America, but it at least seems to be as passable as many other equal-area world maps that have been tried:



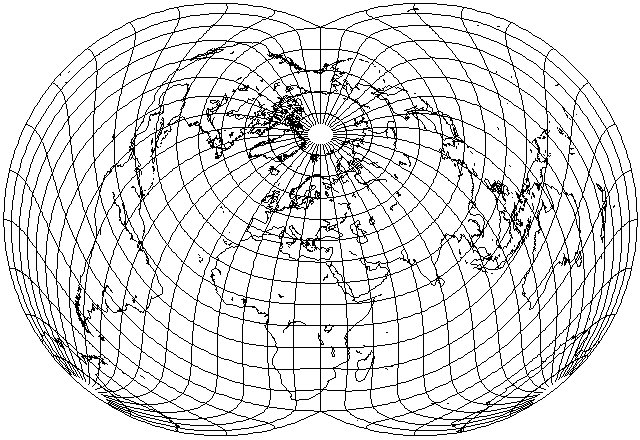
Also, the Dietrich-Kitada projection has ignited my interest in apple-shaped projections in general: one appeared on a computer screen in a James Bond film, and I'm still trying to track that down. In a recent web search, I happened to come across a reference to a truly obscure apple-shaped map projection, by one Henri Bouthillier de Beaumont:



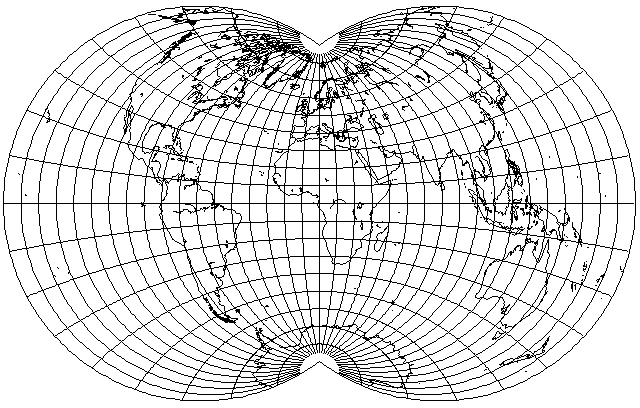
Patented in 1888, it's a modification of the Globular projection, where the boundary of the whole-world map is divided equally.