The Anti-Hammer Projection

[quadibloc]

There is a projection called the Nell-Hammer projection which neither resembles the Hammer projection nor the Nell Globular projection.
Recently probing into the saga of how the Hammer projection got confused with the Aitoff projection, I meditated on Aitoff's statement that in his projection, at least, in contrast to the Hammer, the angular distortion is small enough to no longer be objectionable.
I felt he was an optimist, but I wondered if there was a way to meet his goal.
Giving the Aitoff treatment to the Stereographic seemed to be going overboard. One might as well use Adams' projection of the world on an ellipse, and get real conformality.
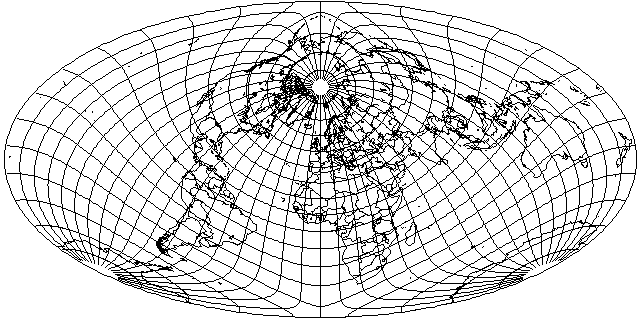
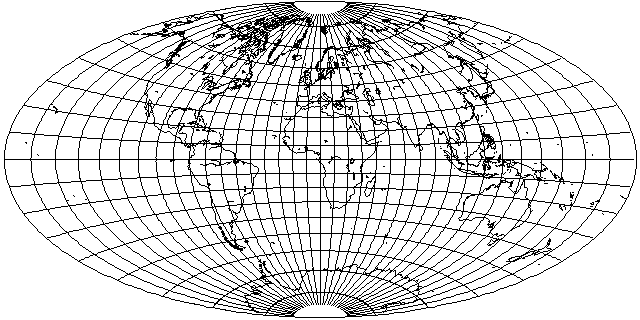
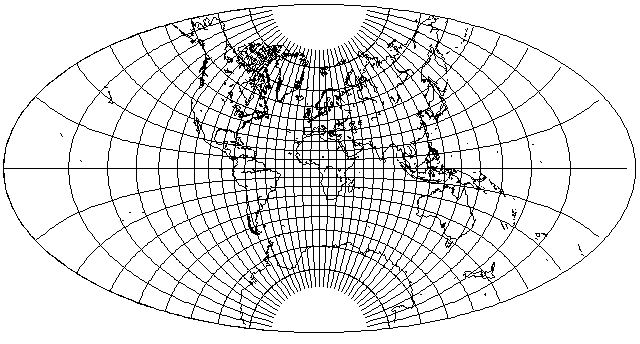
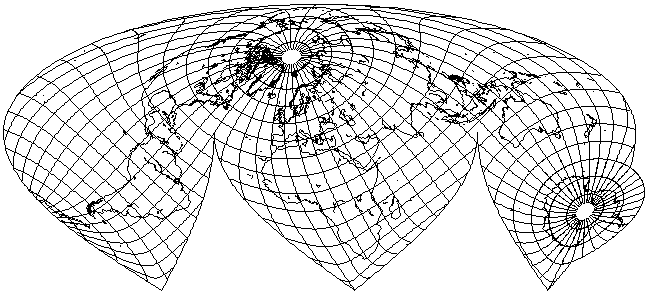
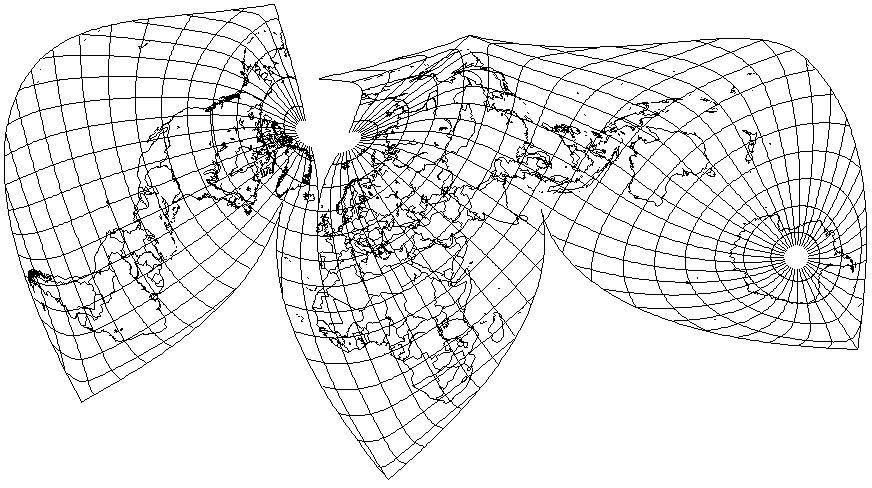
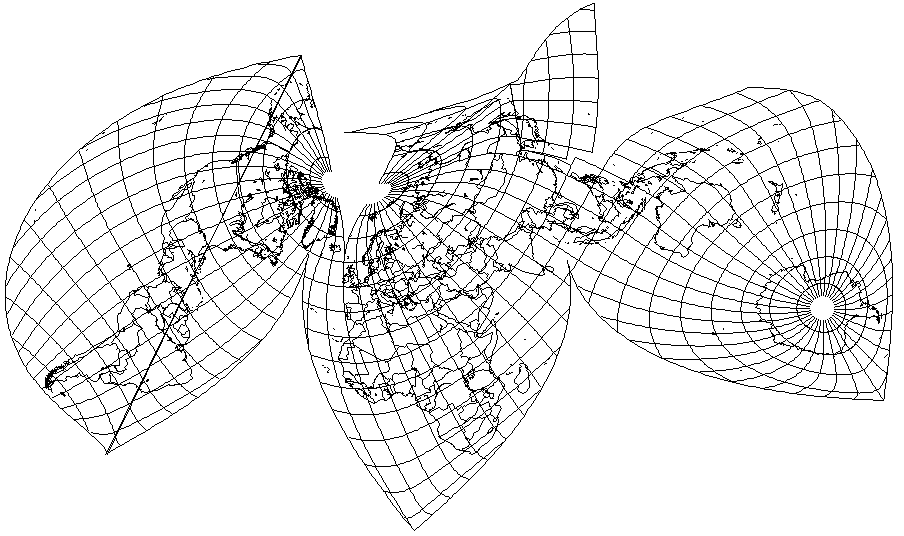
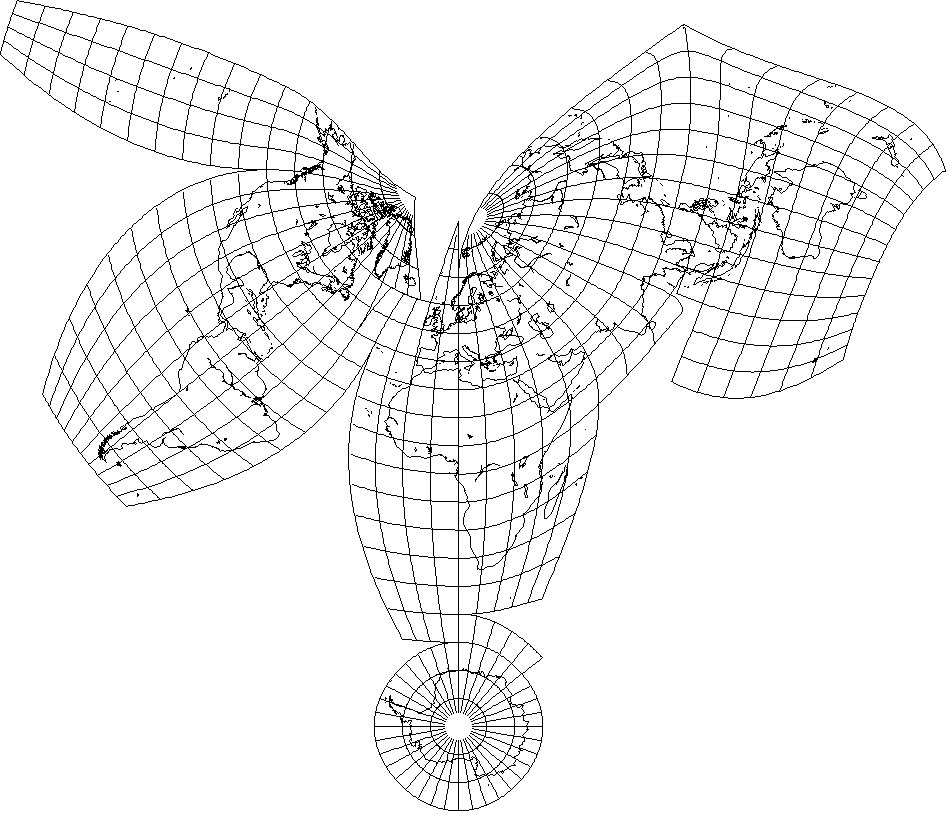
But there is a projection that is sort of halfway between the Azimuthal Equidistant and the Stereographic: Nell's Globular Projection

Somewhat obscure, it is like the Nicolosi Globular projection, but the locations of the points where the parallels cross the central meridian and the meridians cross the Equator are the arithmetic mean of those in the Nicolosi Globular and those in the equatorial case of the Stereographic.
Well, why not give it the Aitoff treatment?

Of course, it goes against current trends, which demand equal-area projections, not ones like the Van der Grinten which lean towards the Mercator in order to look pretty.
And the natural name for it, the Nell-Aitoff, would be potentially confusing, given that there is a Nell-Hammer projection.

[daan]

And the natural name for it, the Nell-Aitoff, would be potentially confusing, given that there is a Nell-Hammer projection.

Giving the Aitoff treatment to the Stereographic seemed to be going overboard.

I’m not so sure. The result would not be conformal, but it would yield parallels that intersect meridians more closely to orthogonal.

— daan

[quadibloc]

I’m not so sure. The result would not be conformal, but it would yield parallels that intersect meridians more closely to orthogonal.

Still, I'm in favor of exaggerating areas as little as possible. This is already good enough for a projection that looks decorative. Of course, since people are used to the Hammer projection, they would expect a projection to a 2:1 ellipse to be equal-area, so this could be more insidious than the Mercator.
It even looks nice in an oblique aspect:

Since you asked, this is what results when you use the Stereographic as a starting point:

Indeed, it is very attractive in appearance.
And, yes, it doesn't exaggerate areas nearly as much as Adams' conformal projection of the world in an ellipse,

so the fact that it isn't conformal isn't a waste, indeed.

[daan]

Meridian duplication on the Nell globular versus on the stereographic is even more subtle than I supposed. Alaskans and New Zealanders might grudgingly appreciate the distinction while complaining about how bad it is regardless.

— daan

[quadibloc]

Alaskans and New Zealanders might grudgingly appreciate the distinction while complaining about how bad it is regardless.

I can make Alaska and New Zealand happy while still having a fully equal-area projection, my take on the Sinu-Bromley:



Unfortunately, though, Hawai'i does not do well. But they could always get an inset map.

[daan]

Unfortunately, though, Hawai'i does not do well. But they could always get an inset map.

They might be tired of being an inset. Nevertheless, I like what you do with the arrangement. Giving Antarctica its own section to avoid being split up works well. I’d probably carve the duplication out of the South American segment, but either way, looks good.

— daan

[quadibloc]

I’d probably carve the duplication out of the South American segment, but either way, looks good.

I considered that. Also, the standard meridian for the segment with Antarctica is wrong.

Actually, instead of just carving the duplication out, I was thinking of moving the whole projection East a bit, but keeping the standard meridian for the Northern Hemisphere where it is, even though it would then be off-center.

So, yes, it's a rough sketch with room for improvement. As you can see, though, my tastes run to keeping angular error very low, and accepting interruptions if I have to in order to obtain that.

I've tried to improve on that by using an interrupted oblique Bonne's, but the best I could manage was this:



which is less pleasing, I fear. I had hoped to gain from curving the parallels upwards, but the pinching of the Bonne near the poles proved to be almost insuperable. I had to use a standard parallel of 15 degrees (my first attempt could use 30) to get Japan out of harm's way. I don't apologize for redrawing some of Eastern Siberia; it gets redrawn at much lower distortion, but of course the copy that's attached should be left in. (In general, I agree with you that duplication is to be avoided.)

In the Americas, the same standard meridian is used both north and south of the standard parallel, so South America can be improved by changing the standard parallel west of that standard meridian. With my mapping program the way it is, though, it's difficult to match the angle so I haven't tried that. Only the stretching of Japan and Korea seems inescapable.

Further thought let me address both issues:



this being a revised version which avoids the need to interrupt Manchuria.

[daan]

That is some pretty crazy interruption and distortion characteristics.

The projection base and interruption scheme remind me of Franz Depuydt’s equivalent quintuple projection. I think his proved rather more successful. His son tells me that Franz’s creation was a reaction to Peters’s promotion of the Gall orthographic.

A variant of his was created by Joeri Theelen:

Theelen equivalent quintuple projection

Theelen Quintuple.png (124.39 KiB) Viewed 1495 times

The differences from Depuydt’s creation are the contiguous path between Australia and Asia, and the (duplicated) Antarctic outset.

— daan

[quadibloc]

The projection base and interruption scheme remind me of Franz Depuydt’s equivalent quintuple projection. I think his proved rather more successful. His son tells me that Franz’s creation was a reaction to Peters’s promotion of the Gall orthographic.

It is very interesting to learn about this projection! I tried to do better with Asia by using an oblique Bonne's instead of a conventional Bonne's as my basis. But either way, this sort of projection is clearly better than the Gall Orthographic, at least in terms of distortion in most places.

Here's another one of mine which does quite a bit better with Asia - but at the expense of Africa.



The Western part is built from conventional Bonne's projections, the Eastern part from oblique ones.

[daan]

I think the first of the September 14th samples is the most successful of these, even ignoring the kinks in the later ones. It gives better fidelity per slice, to my eye. The more slices you allow, the better it should look. With the later renditions, the slicing is as extreme as, say, Cahill’s Butterfly, but to less benefit.

— daan